Exemples
Exemple : Exemple 1
Si \(a\neq0\), la fonction \(x\mapsto ax\) est continue sur \(\mathbf R\) : pour tout \(x_0\in\mathbf R\) et pour tout \(\epsilon> 0\), on peut choisir \(\displaystyle{\eta=\frac{\epsilon}{\vert a\vert}}\).
Si \(a = 0\), la fonction \(x\mapsto ax\) est la fonction nulle.
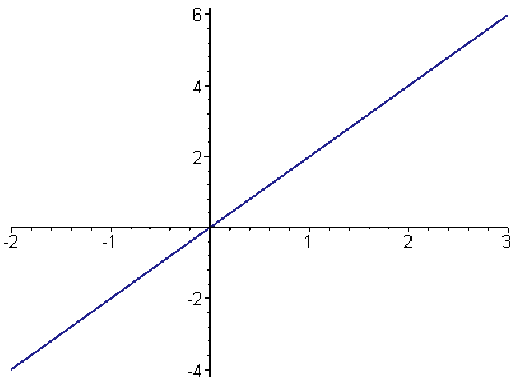
Exemple : Exemple 2
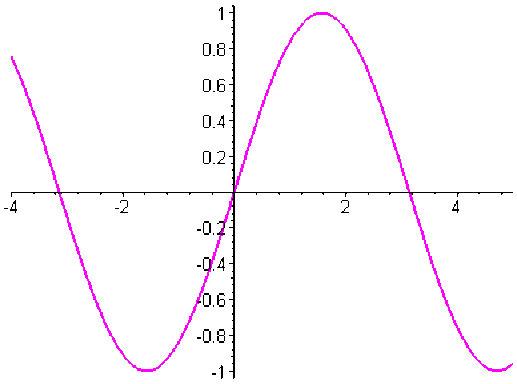
La fonction sinus est continue sur \(\mathbf R\) : pour tout \(x_0\in\mathbf R\) et pour tout\( \epsilon> 0\) on peut prendre \(\eta=\epsilon\),
Exemple : Exemple 3
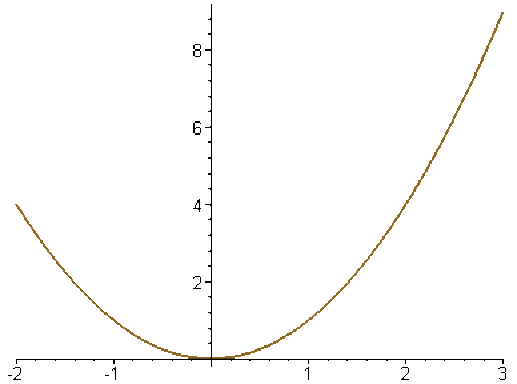
La fonction \(x\mapsto x^2\) est continue sur \(\mathbf R\) : pour tout \(x_0\in\mathbf R\) et pour tout \(\epsilon>0\), on peut prendre \(\displaystyle{\eta=\textrm{min}\left(1,\frac{\epsilon}{2\vert x_0\vert+1}\right)}\).
On remarque ici que notre calcul de \(\eta\) montre que \(x_0\) intervient nécessairement et que l'ensemble \(\displaystyle\left\{\textrm{min}\left(1,\frac{\epsilon}{2\vert x_0\vert+1}\right) ; x_0\in\mathbf R\right\}\) n'a pas de borne inférieure strictement positive.
Exemple : Exemple 4
La fonction partie entière \(\mathcal E\) n'est pas continue sur \(\mathbf R\), ni sur \([0,1]\), elle est, en revanche continue sur \([0,1[\).
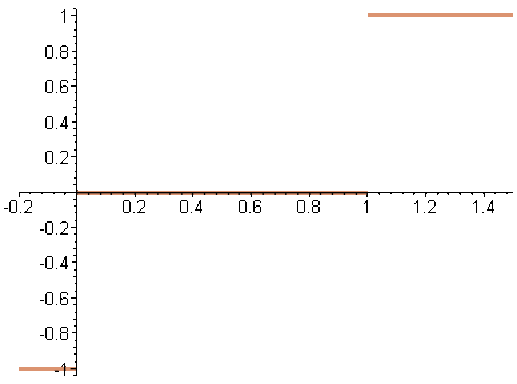
Exemple : Exemple 5
la fonction \(x\mapsto\sqrt x\) est continue sur \([0,+\infty[\).

Exemple : Exemple 6
la fonction exponentielle est continue sur \(\mathbf R\) .
Exemple : Exemple 7
la fonction logarithme est continue sur \(]0,+\infty[\).

La justification complète de la continuité (calcul de \(\eta\) en fonction de \(\epsilon\)) des quatre premières fonctions se trouve dans le cours sur la continuité locale et celle de la continuité des trois dernières (vue en terminale) est reprise dans la partie sur l'étude des fonctions classiques.