Conditions
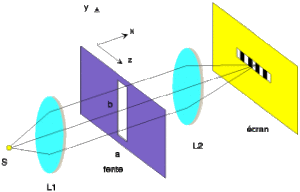
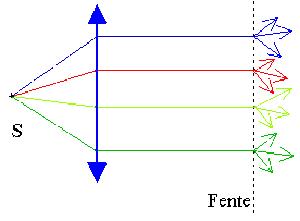
On suppose qu'une fente rectangulaire est éclairée par une onde plane monochromatique.
Elle arrive sous incidence normale pour que tous les points de la fente source soient des sources secondaires en phase, de même amplitude quelle que soit la direction d'émission afin de simplifier le calcul.
La fente a une largeur \(a\) ,une hauteur \(b\).
Soit \(\omega\) la pulsation de l'onde incidente. Chaque point \(M\) de la source fente, repéré par ses coordonnées \((x,y)\), reçoit une vibration lumineuse de la forme :
\(S(x,y) = A_0 ~ \cos(\omega t + \Psi_0)\)
avec \(\Psi_0\) : déphasage par rapport à la source primaire ponctuelle.
Ce point devient une source secondaire émettant de la lumière dans toutes les directions.
Soit \((\mathrm d x . \mathrm d y)\) la surface élémentaire prise autour d'un point \(M\). Cette surface est assez petite pour que tous les points sources secondaires qui la constituent se comportent de manière quasi-identique.
Considérons maintenant l'onde diffractée dans une direction caractérisée par un vecteur unitaire \(\vec u\) et calculons la différence de marche \(\delta\) entre les vibrations arrivant en un point \(P\) à l'infini dans la direction \(\vec u\) (pratiquement en un point \(P\) dans le plan focal image d'une lentille). D'après le principe de Fermat les chemins optiques sont égaux entre un point objet et son point image conjugué dans les conditions de stigmatisme. A chaque direction caractérisée par leur vecteur unitaire \(\vec u\) correspond un seul point image \(P\).