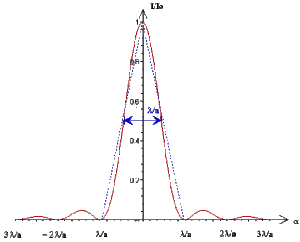
Largeur de la tache principale de diffraction dans le cas d'une fente fine
La tache centrale de diffraction, centrée sur l'image géométrique du point source est plus lumineuse et plus large que les taches latérales.
Calculons sa largeur : le premier minimum nul s'obtient pour \(\alpha = \pm \frac{\lambda}{a}\) soit une largeur \(\Delta \alpha = 2 ~ \frac{\lambda}{a}\)
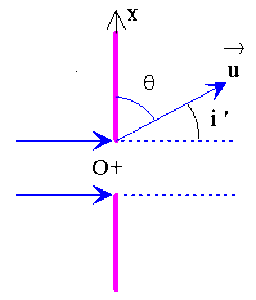
Si \(\alpha\) est petit \(\cos \theta_x\) est faible donc l'angle \(i' = \frac{\pi}{2} - \theta_x\) est petit.
D'où \(\alpha \approx \sin i' \approx i'\) .
La largeur angulaire de la tache de diffraction centrale est dans ce cas \(\Delta i' = 2 ~ \frac{\lambda}{a}\)
Soit dans le plan focal d'une lentille convergente de distance focale \(f '\) :
\(\Delta x' = f' . \Delta i' = 2 f' \frac{\lambda}{a}\)
En admettant que le profil de la tache centrale de diffraction est sensiblement triangulaire on a alors la largeur à mi-hauteur : \(\Delta x' = f' \frac{\lambda}{a}\)
Ce résultat est important car il présente un intérêt pratique.
On remarque que cette tache centrale est d'autant plus large que la largeur de la fente fine est faible.
Si \(a\) augmente la largeur à mi-hauteur diminue. Si \(a\) diminue la largeur à mi-hauteur augmente.
fente de largeur \(a\)
fente de largeur \(a/2\)
fente de largeur \(a/3\)
fente de largeur \(a/4\)
fente de largeur \(a/5\)
fente de largeur \(a/10\)