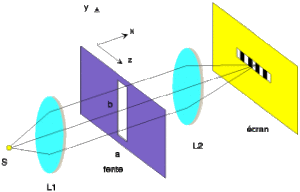
Figure de diffraction
Elle se présente sous la forme suivante pour une fente carrée \(( a = b )\) :

Observation de la figure de diffraction dans le plan focal de la lentille \(L2\) pour une fente carrée
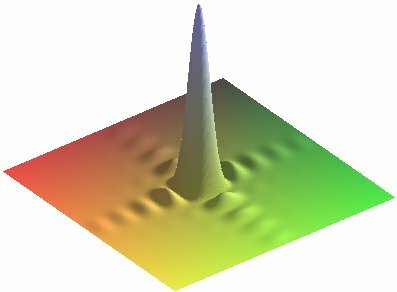
Répartition de l'intensité dans la figure de diffraction
On peut faire les remarques suivantes :
si la fente est fine : \(b \gg a\) par exemple \(a \gg \lambda\) donc \(b \gg \lambda\) .
Les minima s'obtiennent pour \(\beta = k . \frac{\lambda}{b}\) . Donc si \(b\) est grand, les valeurs de \(\beta\) seront très petites et la figure de diffraction se tasse puisque
\(\beta \approx 0\) \(~~ \Rightarrow \cos \theta_y \approx 0\) \(~~ \Rightarrow \theta_y \approx \frac{\pi}{2}\) .
Seule la largeur intervient dans la figure de diffraction qui se réduit alors à une série de point lumineux centrés sur l'image géométrique du point source.

Hauteur double de la largeur : \(b = 2 ~ a\)

Répartition de l'intensité dans la figure de diffraction : \(b = 2 ~ a\)

Hauteur x5 par rapport à la largeur : \(b = 5 ~ a\)

Répartition de l'intensité dans la figure de diffraction : \(b = 5 ~ a\)

Hauteur x 10 par rapport à la largeur : \(b = 10 ~ a\)

Répartition de l'intensité dans la figure de diffraction : \(b = 10 ~ a\)
La diffraction obtenue à partir d'une fente fine est visualisée dans l'animation suivante :