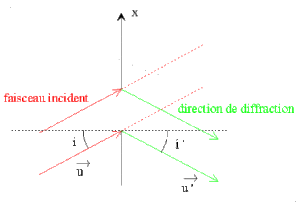
Cas où le faisceau arrive sous une incidence i quelconque et non plus sous incidence normale sur une fente fine
Les calculs précédents restent valables à condition d'écrire :
\(\theta = \overrightarrow{OM} (\vec u - \vec u')\) soit \(\theta = x (\sin i - \sin i')\)