Théorème de superposition / distribution discrète 1/1
Partie
Question
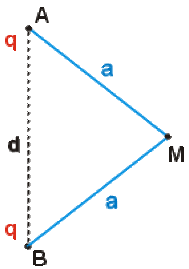
Soient deux charges égales distantes de \(d\), placées à égale distance \(a\) d'un point \(M\). L'objectif de l'exercice est d'exprimer le champ \(E\) existant en \(M\) en fonction de \(q\), \(a\) et \(d\).
Quel est le système de coordonnées le plus adapté à l'étude du problème?
Quelles sont les trois composantes du champ exprimées dans ce système de coordonnées?
Aide simple
----
De façon générale \(\vec E = E_{\rho} ~ \vec u_{\rho} + E_{\theta} ~ \vec u_{\theta} + E_z ~ \vec u_z\)
\(E_{\rho} = \vec E ~ . ~ \vec u_{\rho}\)
\(E_{\theta} = \vec E ~ . ~ \vec u_{\theta}\)
\(E_z = \vec E ~ . ~ \vec u_z\)
Aide détaillée
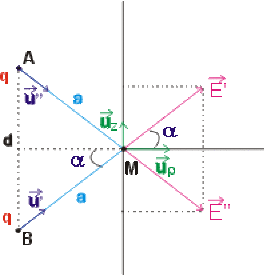
----
Le champ résultant est la somme vectorielle des deux champs \(\vec E'\) et \(\vec E''\) créés par les deux charges.
Solution simple
C'est le système de coordonnées cylindriques autour de l'axe de révolution \(AB\).
\(E_{\rho} = 2.E.\cos \alpha\) ;
\(E_z = E \sin \alpha - E \sin \alpha = 0\) ;
\(E_{\theta}=0\).
Solution détaillée

Le système possède une symétrie de révolution autour de l'axe \(AB\). Il est donc commode d'utiliser les coordonnées cylindriques pour décrire le problème.
\(E_{\rho} = 2.E.\cos \alpha = \frac{2q}{4 \pi \epsilon_0 ~ a^2} \frac{\sqrt{a^2 - \frac{d^2}{4}}}{a}\)
\(E_z = E \sin \alpha - E \sin \alpha = 0\)
\(E_{\theta} = 0\) car le champ se trouve par symétrie dans le plan \(MAB\).
D'où :
\(\vec E = \frac{q}{2 \pi \epsilon_0 ~ a^3} \sqrt{a^2 - \frac{d^2}{4}} ~ . ~ \vec u_{\rho}\)
Le champ est radial.