Champ créé par un fil chargé uniformément 4/4
Partie
Question
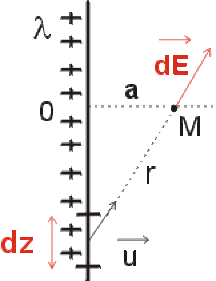
Soit un fil de longueur très grande devant la distance d'observation \(OM = a\).
Ce fil est chargé uniformément par une densité linéique de charge \(\lambda\).
Donner l'expression du champ \(\vec E\) total créé par le fil en fonction de \(\lambda\) et de \(OM = a\).
Aide simple
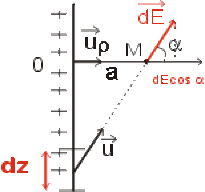
Les variables \(z\), \(\alpha\) et \(r\) sont-elles indépendantes ?
Aide détaillée

Les variables \(z\), \(\alpha\) et \(r\) sont liées : la variation de l'une entraine la variation des deux autres.
\(\tan \alpha = \frac{z}{a}\)
\(a = r ~ \cos \alpha\)
Il ne faut garder dans l'intégrale qu'une seule variable. Il est plus commode d'exprimer \(z\) et \(r\) en fonction de \(\alpha\).
Solution simple
\(\vec E = \frac{\lambda}{2 \pi \epsilon_0 ~ a} \vec u_{\rho}\)
Solution détaillée
\(z = a \tan \alpha\)
D'où :
\(\frac{\mathrm d z}{\mathrm d \alpha} = \frac{a}{\cos^2 \alpha}\)
\(\mathrm d z = \frac{a ~ \mathrm d \alpha}{\cos^2 \alpha}\)
\(r = \frac{a}{\cos \alpha}\)
\(\displaystyle{E = \frac{\lambda}{4 \pi \epsilon_0 ~ a}\int_{-\pi / 2}^{\pi / 2} \cos \alpha \mathrm d \alpha = \frac{\lambda}{2 \pi \epsilon_0 ~ a}}\)
\(\vec E = \frac{\lambda}{2 \pi \epsilon_0 ~ a} \vec u_{\rho}\)