Champ créé par un fil chargé uniformément 1/4
Partie
Question
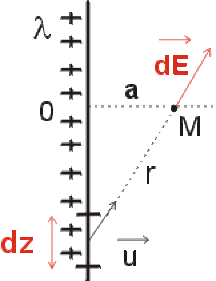
Soit un fil de longueur très grande devant la distance d'observation \(OM = a\).
Ce fil est chargé uniformément par une densité linéique de charge \(\lambda\).
Donner l'expression du champ élémentaire \(\mathrm d \vec E\) créé par un petit élément de longueur \(\mathrm d z\) du fil en un point \(M\) situé à la distance \(r\).
Aide simple
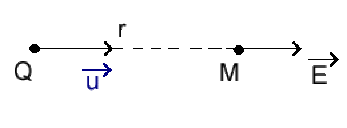
Le champ créé par une charge ponctuelle \(Q\) à la distance \(r\) est :
\(\vec E = \frac{Q}{4 \pi \epsilon_0 ~ r^2} \vec u\)
Aide détaillée
Chaque segment du fil, de longueur \(\mathrm d z\) est chargé d'une densité de charges uniforme \(\lambda\), porte la charge élémentaire \(\mathrm d q = \lambda \mathrm d z\), assimilable à une charge ponctuelle.
Solution simple
\(\mathrm d \vec E = \frac{\lambda \mathrm d z}{4 \pi \epsilon_0 ~ r^2} \vec u\)
Solution détaillée
La formule \(\vec E = \frac{Q}{4 \pi \epsilon_0 ~ r^2} \vec u\) s'applique avec les modifications suivantes : \(\vec E\) est remplacé par \(\mathrm d \vec E\) puisqu'il s'agit d'un champ élémentaire créé par un élément infiniment petit du fil ; \(Q\) est remplacé par \(\lambda \mathrm d z\) puisque chaque segment élémentaire du fil peut être assimilé à une charge ponctuelle \(\mathrm d q = \lambda \mathrm d z\). D'où :
\(\mathrm d \vec E = \frac{\lambda \mathrm d z}{4 \pi \epsilon_0 ~ r^2} \vec u\)