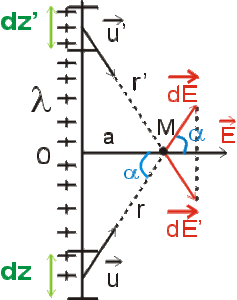
Champ créé par un fil chargé uniformément 3/4
Partie
Question
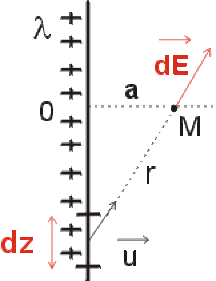
Soit un fil de longueur très grande devant la distance d'observation \(OM = a\).
Ce fil est chargé uniformément par une densité linéique de charge \(\lambda\).
Ecrire l'intégrale permettant de donner le module du champ \(\vec E\) total créé par le fil.
Aide simple
Seules les composantes de \(\mathrm d \vec E\) suivant l'axe \((O, \vec u_r)\) se cumulent.
Aide détaillée
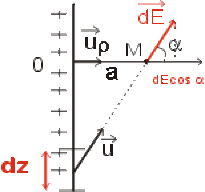
Pour calculer le module de \(\vec E\), il faut intégrer les projections des champs élémentaires \(\mathrm d \vec E\) sur l'axe \(\vec u_r\).
\(\displaystyle{E = \int_{\mathrm{fil}} \mathrm d E \cos \alpha}\)
Solution simple
\(\displaystyle{E = \int_{\mathrm{fil}}\frac{\lambda \mathrm d z}{4 \pi \epsilon_0 ~ r^2}\cos \alpha}\)
Solution détaillée
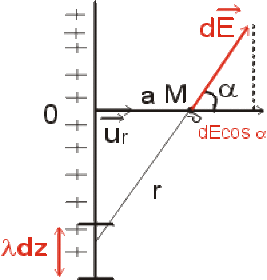
Le champ total étant porté par un axe perpendiculaire au fil, seules les composantes des champs élémentaires \(\mathrm d E\) suivant cet axe doivent être prises en compte.
\(\displaystyle{E = \int_{\mathrm{fil}}\frac{\lambda \mathrm d z}{4 \pi \epsilon_0 ~ r^2}\cos \alpha}\)