Champ E créé par une distribution discrète
Partie
Question

Deux charges \(q\) et \(-2q\) sont distantes de \(a\).
Le champ \(\vec E\) peut-il s'annuler en un point du segment \(AB\)? Si oui, en quel point?
Aide simple
Dessiner les 2 champs respectivement créés par \(q\) et \(-2q\) sous forme de vecteurs, en un point \(M\) du segment \(AB\).
Aide détaillée
Rappelez-vous que dans la formule \(\vec E = \frac{Q}{4 \pi \epsilon_0 ~ r^2} \vec u\), \(\vec u\) est dirigé de la charge source \(Q\) vers le point d'observation. Donnez l'écriture correcte des deux champs respectivement créés par \(q\) et \(-2q\).
Solution simple
Entre \(A\) et \(B\) les deux champs étant colinéaires, leurs contributions s'ajoutent dans le même sens et le champ résultant ne peut s'annuler.
Solution détaillée
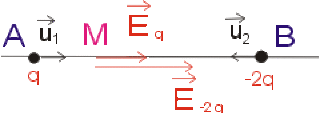
\(\vec E_q = \frac{q}{4 \pi \epsilon_0 ~ (AM)^2} \vec u_1\)
\(\vec E_{-2q} = \frac{-2q}{4 \pi \epsilon_0 ~ (BM)^2} \vec u_2\)
\(\vec u_2 = - \vec u_1\)
\(\vec E = \vec E_q + \vec E_{-2q} = \frac{q}{4 \pi \epsilon_0 ~ (AM)^2} \vec u_1 ~ + ~ \frac{-2q}{4 \pi \epsilon_0 ~ (BM)^2} (- \vec u_1)\)
\(\vec E = \frac{q}{4 \pi \epsilon_0} \Big( \frac{1}{AM^2} + \frac{2}{BM^2} \Big) \vec u_1\) ne peut s'annuler.