Champ créé par un fil chargé uniformément 2/4
Partie
Question
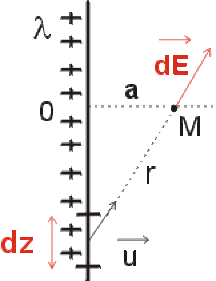
Soit un fil de longueur très grande devant la distance d'observation \(OM = a\).
Ce fil est chargé uniformément par une densité linéique de charge \(\lambda\).
Donner en utilisant les propriétés de symétrie de la structure la direction du champ \(\vec E\) total créé par l'ensemble du fil.
Aide simple
Composez les champs élémentaires \(\mathrm d \vec E\) créés par deux segments du fil uniformément petits, symétriques par rapport à \(OM\).
Aide détaillée
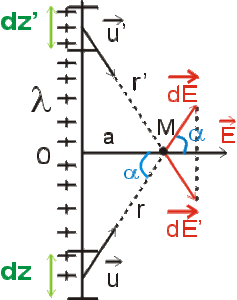
Les champs \(\mathrm d \vec E\) et \(\mathrm d \vec E'\), créés par deux segments du fil symétriques par rapport à \(OM\), sont également symétriques par rapport à \(OM\).
Solution simple
Seules les composantes de \(\mathrm d \vec E\) suivant l'axe \(OM\) se cumulent. Le champ total \(\vec E\) créé par le fil est radial (orthogonal au fil) :
\(\vec E = E ~ \vec u_{\rho}\)
Solution détaillée
L'élément \(\mathrm d z'\) symétrique de \(\mathrm d z\) par rapport à \(OM\) créé un champ \(\mathrm d \vec E'\) symétrique de \(\mathrm d \vec E\) par rapport à \(OM\).
La composition vectorielle de \(\mathrm d E\) et \(\mathrm d E'\) montre que le champ \(\vec E\) résultant est radial.
\(\vec E\) est de la forme \(\vec E = E_r ~ . ~ \vec u_r\)
(\(\vec u_r\) vecteur unitaire d'un axe orienté perpendiculaire au fil)