Relation locale entre E et V
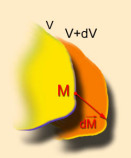
Soient deux surfaces équipotentielles \(V\) et \(V+\mathrm d V\).
Le potentiel est une fonction continue : à un déplacement infiniment petit \(\mathrm d \vec M\) correspond une variation infiniment petite de potentiel \(\mathrm d V\).
La relation intégrale : \(~\displaystyle{V_{A} - V_{B} = - \int_B^A \vec E. \mathrm d \vec M}~\) peut s'écrire compte tenu que : \(V_{A} - V_{B} = \int_B^A \mathrm d V\) en une relation locale :
\(\mathrm d V = - \vec E . \mathrm d \vec M\)
Cette relation permet de déduire le champ \(\vec E\) à partir de la famille de surfaces équipotentielles.