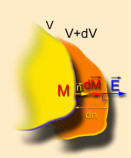
Obtention des lignes de champ E à partir d'une famille d'équipotentielles
On peut tracer les lignes de champ \(\vec E\) à partir d'une famille de surfaces équipotentielles grâce aux propriétés suivantes :
\(\vec E\) est orthogonal aux équipotentielles
Démonstration :
Lors d'un déplacement \(\mathrm d \vec M\) orthogonal à \(\vec E\), on passe d'un point \(M\) à un point \(M'\) tel que \(\vec E . \mathrm d \vec M = 0\)
Donc : \(\mathrm d V = - \vec E . \mathrm d \vec M = 0\)
Les potentiels de \(M\) et \(M'\) sont donc identiques et \(M\) et \(M'\) appartiennent à une même équipotentielle qui est orthogonale au champ.
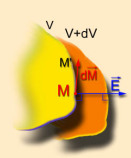
\(\vec E\) est toujours dirigé vers les potentiels décroissants
Démonstration :
Lors d'un déplacement \(\mathrm d \vec M\) colinéaire à \(\vec E\), on passe d'un point \(M\) à un point \(M'\) tel que : \(\mathrm d V = - \vec E . \mathrm d \vec M\)
\(\vec E . \mathrm d \vec M > 0\) donc \(\mathrm d V< 0\). Le champ \(\vec E\) est donc dirigé vers les potentiels décroissants.
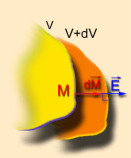
Le long d'une ligne de champ, \(E = - \frac{\mathrm d V}{\mathrm d n}\), où \(\mathrm d V\) est la différence de potentiel entre deux équipotentielles voisines et \(\mathrm d n\) est la distance la plus courte entre ces deux équipotentielles.
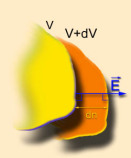
Démonstration :
On définit un vecteur \(\vec n\) normal aux équipotentielles (et donc colinéaire au champ). On peut écrire puisque le champ \(\vec E\) est normal aux équipotentielles : \(\vec E = E ~ \vec n\)
Choisissons d'effectuer un déplacement \(\mathrm d n\) dans la direction de \(\vec n\) (et donc de \(\vec E\))
\(\mathrm d V = - \vec E . \mathrm d \vec M = E ~ \mathrm d n\)
D'où : \(E = - \frac{\mathrm d V}{\mathrm d n}\)
Pour un \(\mathrm d V\) donné, \(E\) est d'autant plus élevé que \(\mathrm d n\) est faible : les zones où les équipotentielles se resserrent correspondent à une zone de champ élevé.