Composantes de E en coordonnées sphériques
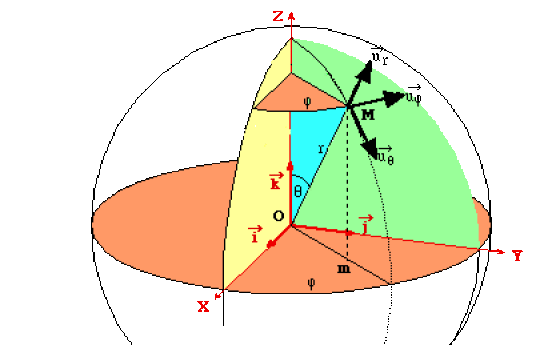
Par analogie avec la démonstration donnée en coordonnées cartésiennes on peut écrire :
Pour un déplacement \(\mathrm d \vec M\) dans la direction radiale \(\vec u_r\) :
\(\overrightarrow{MM'} = \mathrm d \vec M = \mathrm d r ~ \vec u_r\)
soit \(~\mathrm d V = - \vec E~.~\mathrm d \vec M = - \vec E~.~\mathrm d r ~ \vec u_r = - E_r~\mathrm d r\)
\(E_r = - \frac{\partial V}{\partial r}\)
Pour un déplacement \(\mathrm d \vec M\) sur une ligne méridienne :
\(\overrightarrow{MM'} = \mathrm d \vec M = r \mathrm d \theta ~ \vec u_{\theta}\)
soit \(~\mathrm d V = - \vec E~.~\mathrm d \vec M = - \vec E~.~r \mathrm d \theta ~ \vec u_{\theta} = E_{\theta}~r~\mathrm d \theta\)
\(E_{\theta} = - \frac{\partial V}{r ~ \partial{\theta}}\)
Pour un déplacement \(\mathrm d \vec M\) sur un parallèle :
\(\overrightarrow{MM'} = \mathrm d \vec M = r \sin \theta ~ \mathrm d \phi ~ \vec u_{\phi}\)
soit \(~\mathrm d V = - \vec E~.~\mathrm d \vec M = - \vec E~.~r \sin \theta ~ \mathrm d \phi ~ \vec u_{\phi} = E_{\phi}~r \sin \theta~\mathrm d \phi\)
\(E_{\phi} = - \frac{\partial V}{r \sin \theta~\partial \phi}\)