Signification physique du gradient
Revenons sur la notion de gradient et sur sa signification physique.
On peut associer un vecteur gradient à toute fonction continue de points.
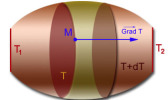
Prenons l'exemple d'un matériau ayant une forme allongée et imposons des températures constantes, \(T_1\) et \(T_2\) ( \(T_1 \ne T_2\) ) , à ses extrémités. Après un certain temps, l'équilibre thermique est réalisé : la température reste constante en chaque point du matériau, mais elle varie évidemment d'un point à un autre. La température est donc dans ce matériau une fonction de la position du point d'observation.
Une surface isotherme, \(T\), est le lieu des points où la température a la valeur \(T\).
Pour définir le vecteur \(\overrightarrow{\mathrm{grad}}~T\) en un point \(M\) du matériau considérons la surface isotherme \(T\) passant par ce point et la surface isotherme infiniment voisine, \(T + \mathrm d T\).
Le vecteur, \(\overrightarrow{\mathrm{grad}}~T\), est porté par la normale en \(M\) à la surface isotherme, \(T\). C'est suivant cette direction que la variation de température est la plus rapide, autrement dit que le gradient de température est le plus élevé.
Considérons en effet des déplacements à partir d'un point quelconque \(P\) sur la surface isotherme \(T\) jusqu'en des points de la surface isotherme \(T + \mathrm d T\). La variation correspondante de température a pour ces déplacements la même valeur \(\mathrm d T\).
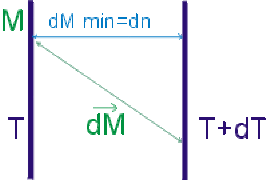
Remarquons que la longueur des déplacements est variable et est minimale suivant la direction de la normale. C'est donc suivant cette direction que la variation de température est la plus rapide.
On la caractérise par le rapport \(\frac{\mathrm d T}{\mathrm d n}\) de l'augmentation de température, \(\mathrm d T\), à la distance minimale, \(\mathrm d n\), qu'il faut parcourir pour l'observer.
Par définition le module du vecteur \(\overrightarrow{\mathrm{grad}}~T\) est égal à ce rapport.
Enfin, on convient de l'orienter dans le sens des valeurs croissantes de la température.