Composantes de E en coordonnées cartésiennes
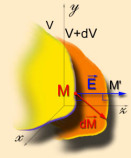
Choisissons un système d'axes rectangulaires \((Ox, Oy, Oz)\) et considérons que le potentiel \(V(M)\) est une fonction des coordonnées \(x, y, z\) du point \(M\).
Le vecteur \(\vec E\) (vecteur champ électrique au point \(M\)), est orthogonal aux équipotentielles. La variation \(\mathrm d V\) du potentiel au voisinage du point \(M\) est donnée par : \(\mathrm d V = - \vec E . \mathrm d \vec M\)
Soit le cas particulier d'un déplacement \(\mathrm d \vec M\) parallèle à l'axe \(Ox\) et de même sens que cet axe. Si le point \(M\) a les coordonnées \((x, y, z)\) le point \(M'\) a les coordonnées \((x+dx, y, z)\) et par suite \(\overrightarrow{MM'} = \mathrm d \vec M = \mathrm d x ~ \vec i\) où \(\vec i\) désigne le vecteur unitaire de l'axe \(Ox\).
La formule précédente peut s'écrire : \(\partial V = - \vec E ~ \partial x ~ \vec i\) soit : \(\frac{\partial V}{\partial x} = - \vec E . \vec i = - E.x\)
Le premier membre est égal au rapport de la variation de potentiel \(\partial V\) (dans le cas particulier d'un déplacement parallèle à l'axe \(Ox\)) et de ce déplacement \(\partial x\). Ce rapport est appelé dérivée partielle[1] de la fonction \(V\) par rapport à la variable \(x\) et il est désigné par \(\frac{\partial V}{\partial x}\) .
Le second membre est la composante du vecteur \(\vec E\) suivant \(Ox\). On ferait les raisonnements analogues en considérant des déplacements élémentaires parallèles aux axes \(Oy\) et \(Oz\).Les composantes de \(\vec E\) sur les axes \(Ox, Oy, Oz\) sont donc égales aux dérivées partielles de la fonction \(V\) par rapport aux variables \(x\), \(y\), et \(z\).
\(E_x = - \frac{\partial V}{\partial x}\)
\(E_y = - \frac{\partial V}{\partial y}\)
\(E_z = - \frac{\partial V}{\partial z}\)