Fentes d'Young (5)
Partie
Question
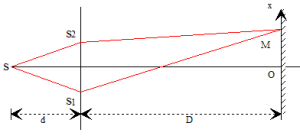
On considère deux fentes d'Young \(S_1\) et \(S_2\) distantes de \(2a\) éclairées en lumière monochromatique de longueur d'onde dans le vide \(\lambda\) par une fente source \(S\) parallèle et équidistante aux fentes \(S_1\) et \(S_2\). Soit \(d\) la distance de \(S\) au plan des fentes, \(D\) la distance du plan des fentes au plan d'observation. \((P)\) parallèle au plan des fentes. Le dispositif est placé dans l'air (\(n=1\)).
La source \(S\) est maintenant translatée d'une quantité \(l_1\) vers \(S_1\). que deviennent \(\delta'_3\) et \(i'_3\) ?
Solution détaillée
\(\delta'_3=(SS_1)+(S_1M)-(SS_2)-(S_2M)\)
\(SS_1-SS_2=-\frac{S_1S_2.l_1}{d}\) avec \(l_1<<d\,\, et \,\,S_1S_2<<d\)
Le calcul est identique à celui qui a été fait pour \(S_1M\) - \(S_2M\)
d'où \(\delta'_3=\delta-S_1S_2\frac{l_1}{d}=\frac{S_1S_2.x}{D}-S_1S_2\frac{l_1}{d}\)
Pour la frange d'ordre \(k=0\), \(\delta'_3=k.d=0=\frac{S_1S_2.x_0}{D}-S_1S_2\frac{l_1}{d}\)
d'où \(x_0=+l_1\frac{D}{d}\)
La frange centrale se déplace du côté de \(S_2\). En ce qui concerne l'interfrange \(i'_3\):
\(\Delta k.\lambda=\Delta(\delta'_3)=\frac{S_1S_2.\Delta x}{D}\)
si \(\Delta k=1\) et \(\Delta x=i'_3\) alors
\(i'_3=\frac{\lambda.D}{S_1S_2}=i\)
L'interfrange est bien sûr inchangé.