Miroir de Lloyd (2)
Partie
Question
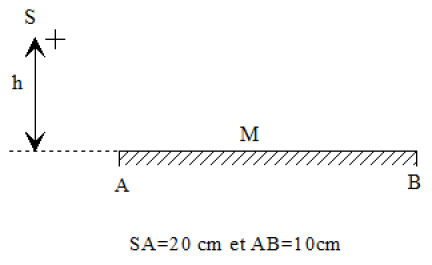
Une lame de verre plane \((M)\) est éclairée sous incidence rasante par une source ponctuelle \(S\) placée à une faible distance \(h =\mathrm{1 mm}\) au dessus du plan de la lame. Cette source émet une lumière monochromatique de longueur d'onde \(\lambda= \textrm{546 nm}\).
Calculer l'interfrange (en mm)
Aide simple
La réflexion vitreuse (d'un milieu moins réfringent sur un milieu plus réfringent) introduit une différence de marche physique supplémentaire de \(l/2\).
Solution détaillée
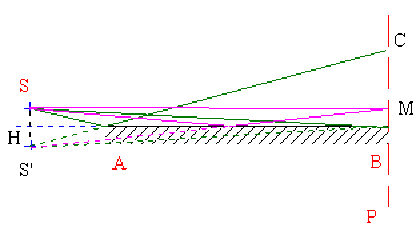
En un point \(M\) du plan \(P\) situé à la distance \(BM = x\) la différence de marche entre les ondes qui interfèrent est :
\(\delta=\frac{SS'.x}{HB}+\frac{\lambda}{2}\)
En \(B\) (\(x=0\)) donc \(\delta=\frac{\lambda}{2}\) et il y a une frange noire
L'interfrange vaut \(i=\frac{\lambda.HB}{SS'}\)
A.N : \(i=\textrm{0,082 m}\)