Fentes d'Young (4)
Partie
Question
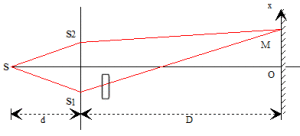
On considère deux fentes d'Young \(S_1\) et \(S_2\) distantes de \(2a\) éclairées en lumière monochromatique de longueur d'onde dans le vide \(\lambda\) par une fente source \(S\) parallèle et équidistante aux fentes \(S_1\) et \(S_2\). Soit \(d\) la distance de \(S\) au plan des fentes, \(D\) la distance du plan des fentes au plan d'observation. \((P)\) parallèle au plan des fentes. Le dispositif est placé dans l'air (\(n=1\)).
Pour le même dispositif on place une lame fine à faces parallèles d'épaisseur \(e\) devant la source \(S_1\). Déterminer \(\delta'_2\) et \(i_2\). A.N: \(e = \mathrm{2 mm}, n =\mathrm{1,5}\).
Aide simple
Refaire les mêmes calculs qu'en l'abscence de la lame à faces parallèles
Rappel de cours
Voir la page Fentes d'Young
Solution détaillée
\(\delta'_2=(S_2M)-(S_1M)\) avec \((S_2M)=S_2M=d_2\)
Sur le trajet \(S_1M\) une épaisseur \(e\) d'air \(a\) été remplacée par une lame d'épaisseur \(e\) d'indice \(n\). Donc on a un trajet optique plus grand pour \(S_1M\).
\((S_1M)=d_1-e+n\,e=d_1+e(n-1)\)
La quantité \(e ( n - 1 )\) est constante donc \(\delta'_1=d_1-d_2+e(n-1)=\delta+e(n-1)\)
Pour la frange d'ordre \(k = 0\) \(\delta'_2=k\lambda=0=\frac{S_1S_2.x_0}{D}+e(n-1)\)
d'où \(x_0=-e(n-1)\frac{D}{S_1S_2}\)
la frange centrale a subi une translation du côté de \(S_1\) Le système de franges s'est simplement déplacé.
Concernant l'interfrange \(i'_2\) nous avons :
\(\Delta k\,d=\Delta(\delta'_1)=S_1S_2\,\frac{\Delta x}{D}\)
si \(\Delta k=1 \,et\, \Delta x=i\) alors \(i'_2=i\)
le système de frange s'est simplement déplacé.
A.N : \(x_0=- \frac{2.10^{-3}.0,51}{10^{-3}}=- 1mm\)