Fentes d'Young (1)
Partie
Question
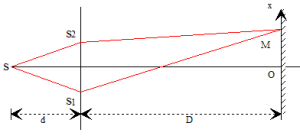
On considère deux fentes d'Young \(S_1\) et \(S_2\) distantes de \(2a\) éclairées en lumière monochromatique de longueur d'onde dans le vide \(\lambda\) par une fente source \(S\) parallèle et équidistante aux fentes \(S_1\) et \(S_2\). Soit \(d\) la distance de \(S\) au plan des fentes, \(D\) la distance du plan des fentes au plan d'observation. \((P)\) parallèle au plan des fentes. Le dispositif est placé dans l'air (\(n=1\)).
a) Calculer la différence de marche en un point \(M\) de l'écran repéré par son abscisse x.
Aide simple
Evaluer la différence entre les trajets optiques \(SS_1M\) et \(SS_2M\)
Rappel de cours
Voir la page Fentes d'Young
Solution détaillée
\(\delta=(SS_1)+(S_1M)-(SS_2)-(S_2M)\)
ici \((SS_1)=(SS_2)=SS_1.n=SS_1\) car \(n=1\)
\(\delta=S_1M-S_2M\simeq\frac{S_1S_2.x}{D}\)