Fentes d'Young (3)
Partie
Question
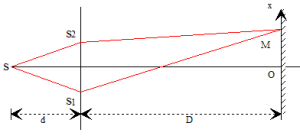
On considère deux fentes d'Young \(S_1\) et \(S_2\) distantes de \(2a\) éclairées en lumière monochromatique de longueur d'onde dans le vide \(\lambda\) par une fente source \(S\) parallèle et équidistante aux fentes \(S_1\) et \(S_2\). Soit \(d\) la distance de \(S\) au plan des fentes, \(D\) la distance du plan des fentes au plan d'observation. \((P)\) parallèle au plan des fentes. Le dispositif est placé dans l'air (\(n=1\)).
c) Le même dispositif est plongé entièrement dans un milieu transparent d'indice \(n=\mathrm{1,5}\). Calculer \(\delta'_1\) et \(i_1\).
Aide simple
Tenir compte de l'indice du milieu pour la détermination de l'interfrange.
Rappel de cours
Voir la page Fentes d'Young
Solution détaillée
Calculer de \(\delta'_1\) et \(i_1\):
\(\delta'=(S_1M)-(S_2M)\) avec \((S_1M)=n.S_1M=n.d_1\) et \((S_2M)=n.S_2M=n.d_2\)
\(\delta'_1=n.\delta=n(d_1-d_2)=n\frac{S_1S_2.x}{D}\)
On remarque que \(n=\frac{c}{v}\) , \(v\) étant la vitesse de propagation de l'onde dans le vide.
\(\lambda_{vide}=c.T=c\frac{2\pi}{\omega}\)
\(\lambda_n=v\frac{2\pi}{\omega}=\frac{c}{n}\frac{2\pi}{\omega}=\frac{\lambda_{vide}}{n}\)
La longueur d'onde dépend du milieu considéré mais la pulsation est une caractéristique indépendante du milieu.
Le trajet optique est la distance \(( d )\) parcourue dans le vide pendant le temps \(t\) que la vibration met pour parcourir une distance \(d\) dans le milieu d'indice n.
\(t=\frac{d}{v}=\frac{d}{\frac{c}{n}}=\frac{nd}{c}=\frac{(d)}{c}\)
d'où \((d)=nd\)
La frange centrale est obtenue pour \(\delta'_1=n\frac{S_1S_2}{\lambda}\) avec \(x=0\)
\(\delta'_1=k\lambda \Rightarrow k=0\) qui correspond à la frange d'ordre \(0\)
D'après la définition de l'interfange
\(n\frac{S_1S_2}{D}.i'_1=\lambda \Rightarrow i'_1=\frac{\lambda D}{n\, S_1S_2}=\frac{i}{n}\)
L'interfrange diminue d'un facteur \(\mathrm{1,5}\)