Pendule simple
Partie
Question
Pendule simple (*)
Un pendule simple est constitué d'une boule sphérique de rayon r, de masse m suspendue par un fil de masse négligeable, de longueur l; l'autre extrémité du fil est accrochée à un point fixe \(O\). On prendra\( l \gg r\) de telle sorte que la boule pourra être assimilée à un point matériel. Le système est dans le champ de pesanteur terrestre et on néglige tout frottement.
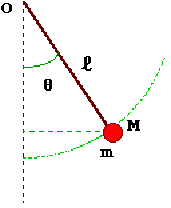
On étudie le mouvement dans le plan vertical Oxy d'un référentiel local supposé galiléen pour la durée du mouvement.
Faire le bilan des forces appliquées à la boule.
On utilise un repérage cartésien \(M(x,y)\). Etablir l'équation du mouvement à l'aide du principe fondamental de la dynamique.
On utilise un repérage polaire \(M(l,\theta)\) avec \(\displaystyle{\theta=(\overrightarrow{Ox},\overrightarrow{OM})}\).
Calculer le moment cinétique de la boule par rapport à \(O\). En déduire l'équation du mouvement en appliquant le théorème du moment cinétique .
Etudier le cas des petites oscillations ( \(sin\theta\) de l'ordre de \(\theta\)).
Aide simple
Utiliser le théorème du moment cinétique par rapport au point O
Solution détaillée
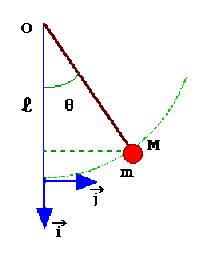
La masse \(m\) est soumise au poids \(\displaystyle{\overrightarrow p=mg\overrightarrow i}\) et à la tension du fil
\(\displaystyle{\overrightarrow T=-\frac{T}{l}\overrightarrow{OM}=-\frac{T}{l}(x\overrightarrow i+y\overrightarrow j)}\)
La relation fondamentale de la dynamique s'écrit :
\(\displaystyle{m(x"\overrightarrow i+y"\overrightarrow j)=mg\overrightarrow i-\frac{T}{l}(x\overrightarrow i+y\overrightarrow j)}\)
soit :
\(\displaystyle{mx"=mg-\frac{T}{l}x\textrm{ et }my"=-\frac{T}{l}y}\)
Moment cinétique :
\(\displaystyle{\overrightarrow\sigma=\overrightarrow{OM}\wedge m\overrightarrow V=1\overrightarrow u_{\rho}\wedge ml\theta'\overrightarrow u_\theta=ml^2\theta'(\overrightarrow u_\rho\wedge\overrightarrow u_\theta)\textrm{ soit }\overrightarrow\sigma=ml^2\;\theta'\overrightarrow k}\)
Par application du théorème du moment cinétique :
\(\displaystyle{\frac{\textrm d\overrightarrow\sigma}{\textrm dt}=\overrightarrow{OM}\wedge\overrightarrow F=1\overrightarrow u_\sigma\wedge(-T\overrightarrow u_\rho+mg\overrightarrow i)}\)
\(\displaystyle{\frac{\textrm d}{\textrm dt}(ml^2\theta'\overrightarrow k)=mgl\overrightarrow u_\rho\wedge\overrightarrow i=mgl(\cos\theta\overrightarrow i+\sin\theta\overrightarrow j)\wedge\overrightarrow i}\)
\(\displaystyle{ml^2\theta"\overrightarrow k=-mgl\sin\theta\overrightarrow k}\)
d'où : \(\displaystyle{\theta"=-\frac{g}{l}\sin\theta}\)
Avec\( \displaystyle{\sin\theta\approx\theta}\),
et en posant : \(\displaystyle{\omega^2=\frac{g}{l} :\theta"+\omega^2\theta = 0}\) dont la solution est : \(\theta = \theta_0\cos(\omega t + \phi)\)