Le choc était comment ?
Partie
Question
Le choc était comment ? (*)
Deux boules identiques, de masse m, glissent sans frottement sur un plan.
La boule \(B\) initialement au repos, est heurtée par la boule \(A\) dont la vitesse \(v\) est de \(4\) mètres par seconde.
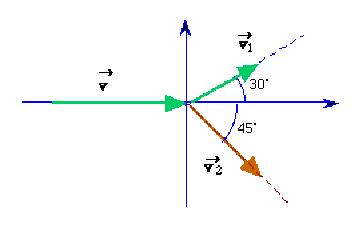
Après le choc, les trajectoires de \(A \textrm{ et }B\) sont respectivement à \(30° \textrm{ et }45°\) de la trajectoire incidente.
Trouver les vitesses des boules après le choc. Ce choc est-il parfaitement élastique, partiellement élastique ou parfaitement mou ?
Aide simple
La conservation de l'énergie cinétique caractérise les chocs élastiques
Solution détaillée
On appelle \(\displaystyle{\overrightarrow v_1\textrm{ et }\overrightarrow v_2}\) et les vitesses après le choc des boules.
Le système des deux boules est isolé, il y a conservation de la quantité de mouvement.
On considère les projections des quantités de mouvement suivant deux directions : celle de \(\overrightarrow v\) et sa perpendiculaire:
\(\begin{array}{rcl}mv_1\cos30°+mv_2\cos45°&=&mv\\mv_1\cos60°-mv_2\cos45°&=&0\end{array}\)
Soit en valeurs numériques:
\(\begin{array}{rcl}v_1\sqrt{3}+v_2\sqrt2&=&2v\\ v_1-v_2\sqrt2&=&0\end{array}\)
\(\displaystyle{v_1=\frac{2v}{\sqrt3+1}\textrm{ et }v_2=\frac{v\sqrt2}{\sqrt3+1}}\)
Avec la valeur de \(v\) donnée on trouve
\(\displaystyle{v_1=2,93\textrm{ ms}^{-1}\textrm{ et }v_2=2,07\textrm{ ms}^{-1}}\)
Calculons les énergies cinétique initiale et finale du système:
\(\displaystyle{T_i=\frac{1}{2}mv^2\textrm{ et }T_f=\frac{1}{2}m(v_1^2+v_2^2)=mv^2(\frac{3}{\sqrt2+2})}\)
\(T_f < T_i\)
Le choc est partiellement inélastique, puisque l'énergie cinétique finale est inférieure à l'initiale.