Théorèmes généraux

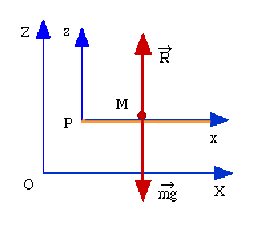
On lie au plateau \(P\) un référentiel (\(P,x,z\)). On lie au sol un référentiel (\(O,X,Z\)) et on le suppose galiléen.

Dans (\(O,x,z\)) galiléen, le principe fondamental de la dynamique s'écrit :

\(\displaystyle{m(\overrightarrow{\gamma/P}+\overrightarrow\gamma_e+\overrightarrow\gamma_c)=m\overrightarrow g+\overrightarrow R}\)

Il n'y a pas de rotation du plateau, donc l'accélération de Coriolis est nulle :

\(\displaystyle{(\overrightarrow\omega_e=\overrightarrow0)\textrm{ et }\overrightarrow\gamma_c=\overrightarrow0}\) ;

l'accélération d'entraînement se réduit à -\(\omega^2a\cos \omega t\) car le mouvement du plateau dans (\(O,X,Z\)) est donné par:

\(Z = a \cos \omega t\) ce qui implique\( Z'' = - \omega^2a \cos \omega t\)

L'accélération du plateau dans (\(O,X,Z\)) s'écrit ,

\(\displaystyle{\omega^2a\cos\omega t\overrightarrow k}\)

par suite :

\(\displaystyle{m\overrightarrow{\gamma/P}-m\omega^2a\cos\omega t\overrightarrow k=m\overrightarrow g+\overrightarrow R}\)

On veut que le point matériel soit en équilibre sur le plateau donc \(\displaystyle{\overrightarrow{\gamma/P}=\overrightarrow0}\) ,

\(\displaystyle{m\overrightarrow g+\overrightarrow R+m\omega^2a\cos\omega t\overrightarrow k=\overrightarrow0}\)

\(\displaystyle{-mg+R+m\omega^2a\cos\omega t}\)

\(\displaystyle{R=mg-m\omega^2a\cos\omega t}\)

La masse décolle du plateau lorsque la réaction s'annule, soit :

\(0 = mg - m \omega^2 a \cos \omega t\)

La pulsation est alors donnée par :

\(\displaystyle{\omega^2=\frac{g}{a\cos\omega t}}\)

Cette relation doit être satisfaite à tout instant; la valeur minimale de \(\omega\) à ne pas dépasser est celle qui correspond à

\(\cos \omega t\) maximum, soit

\(\displaystyle{\cos\omega t=1\textrm{ et }\omega\leq\sqrt{\frac{g}{a}}}\)

A.N. \(\omega = 14 \textrm{ rad.s}^{-1}, \textrm{ période }T = 0,45 \textrm{ s}, \textrm{ fréquence }f = 2,23 \textrm{ Hz}\)