Formule de conjugaison du dioptre plan [Dioptre plan]

Formule de conjugaison du dioptre plan

Nous avons précédemment noté que l'image ^[1]à travers un dioptre plan d'un objet ^[2]situé à l'infini est un point également situé à l'infini. De même, lorsqu'un point objet appartient à la surface du dioptre, son image ponctuelle est parfaitement positionnée puisque les deux points sont confondus.

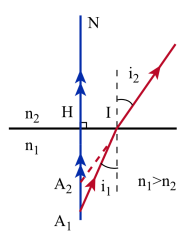
Dans le cas plus général où le point source A₁ est situé à distance finie et satisfait à la condition de stigmatisme ^[3]approché, on a établi que : \(\overline{\mathrm{HA}_2}=\overline{\mathrm{HA}_1}~\frac{\mathrm n_2}{\mathrm n_1}\)

à condition que les angles i₁et i₂ soient suffisamment petits.

Généralement exprimée sous la forme : \(\frac{\mathrm n_1}{\overline{\mathrm{HA}_1}}=\frac{\mathrm n_2}{\overline{\mathrm{HA}_2}}\)

cette relation constitue la formule de conjugaison du dioptre plan.

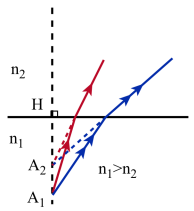
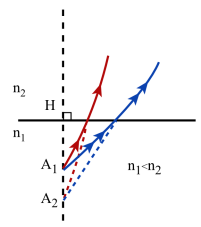
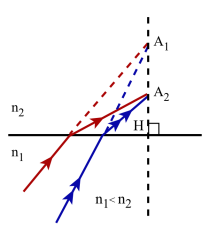
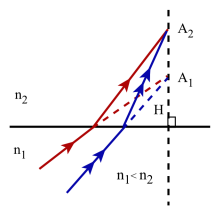
Outre son intérêt pour déterminer mathématiquement les positions relatives de l'objet ^[2]et de son image^[1] par rapport au dioptre, cette formule permet de préciser certaines données qualitatives. En effet on sait que les indices n₁et n₂ sont des grandeurs positives; par conséquent \(\overline{\mathrm{HA}_1}\) et \(\overline{\mathrm{HA}_2}\) ne peuvent être que de même signe.

Ceci signifie que :

pour un couple de points conjugués ^[4]A₁ et A₂ appartenant, optiquement parlant aux milieux d'indices respectifs n₁ et n₂

- A₁ et son image A₂ sont toujours situés sur la même normale au dioptre
- A₁ et son image A₂ sont toujours situés du même côté du dioptre
- A₁ et son image A₂ sont toujours de nature différente: si l'un est réel, l'autre est virtuel et réciproquement
- si n₁ > n₂ , A₁ est toujours plus éloigné de la surface du dioptre que A₂ ; inversement si n₁ < n₂ , A₁ est toujours plus proche de cette surface que A₂.

Notes

Image
On appelle image d'un objet par un système optique, l'ensemble des images des points de l'objet.
On appelle image d'un point, la zone de convergence des rayons, après traversée du système optique (image réelle) ou la zone d'où les rayons semblent provenir (image virtuelle). Lorsque cette zone se réduit à un point, le système est dit stigmatique.
En pratique, l'image ressemble à l'objet (sinon le système ne présente pas d'intérêt), elle peut être
- agrandie : plus grande que l'objet ( |grandissement| >1) ;
- rapetissée : plus petite que l'objet ( |grandissement| <1) ;
- droite : dans le même sens que l'objet (grandissement >0) ;
- renversée : dans le sens contraire à l'objet (grandissement <0) ;
- déformée : un système qui déforme parce qu'il n'a pas le même grandissement dans différentes directions provoque une anamorphose (ex : glace déformante) ;
- floue
Objet
En optique, on appelle objet tout ensemble de points lumineux. Il peut s'agir d'une source primaire qui produit de la lumière (ex : soleil, étoiles, filament de lampe allumée, écran de télévision ou d'ordinateur en fonction), ou d'une source secondaire qui diffuse une partie de la lumière qu'elle reçoit (ex : lune, planètes, la plupart des objets qui nous entourent lorsqu'ils sont éclairés).
On considère, en général, des objets plans situés dans des plans de front de systèmes optiques.
Dans des systèmes composés on pourra considérer qu'une image produite par une première partie du système est un objet pour le reste du système.
Stigmatisme
Propriété d'un système optique qui associe un seul point image à un seul point source. Un système peut n'être stigmatique que pour certains points remarquables. Pour un système stigmatique, tous les rayons issus d'un point source du domaine de stigmatisme, convergent vers le (ou proviennent du) même point image. Le stigmatisme est dit rigoureux lorsque le chemin optique entre le point objet et le point image est indépendant du rayon. Le stigmatisme est dit approché lorsque les conditions de Gauss sont nécessaires pour qu'il soit réalisé.
Exemple de système non stigmatique pour le couple de points \(AA'\) : le rayon \(APP"A"\) ne passe pas par \(A'\), image de \(A\) par d'autres rayons.
Un dioptre plan n'est pas stigmatique.
Conjugués
Les points A et A' sont dits conjugués, par un système optique, lorsque A' est l'image de A. Le système est alors stigmatique pour les points A et A'.
Les plans P et P' sont dits conjugués, lorsque tout point du plan P possède une image dans le plan P'.