Applications
Prisme à réflexion totale
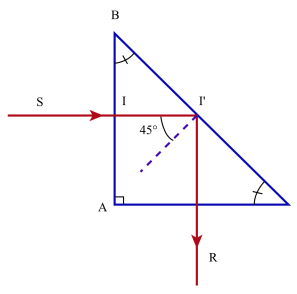
Considérons un prisme de verre dont la section droite est un triangle rectangle isocèle et un rayon incident SI qui pénètre normalement la face d'entrée du prisme; il n'est pas dévié et atteint la face hypoténuse du prisme sous un angle de 45° qui est supérieur à l'angle limite (voisin de 42°). Il est donc totalement réfléchi et ressort par la face AC du prisme sans être dévié par celle-ci.
Le prisme s'est donc comporté pour le rayon SI comme un miroir plan parfait suivant sa face hypoténuse.
Le prisme à réflexion totale remplace le miroir plan dans beaucoup d'instruments d'optique (périscope) car son pouvoir réflecteur est plus grand sans qu'il soit nécessaire de déposer sur le verre une couche métallique réfléchissante pouvant s'altérer au contact des agents atmosphériques.
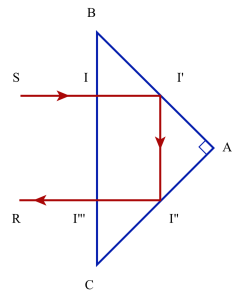
Dans certains instruments d'optique, comme les jumelles, les rayons incidents sont normaux à la face hypoténuse du prisme et sont donc renvoyés dans la direction incidente après avoir subis deux réflexions totales.
Fontaines lumineuses ; fibres optiques


La forme du jet d'eau sortant du récipient rempli d'eau est telle que le rayon incident SI est réfléchi totalement en A, B et C. Ce qui permet de guider la lumière dans un écoulement d'eau et ainsi réaliser des fontaines lumineuses.
On peut également guider la lumière à travers une baguette de verre ou de plexiglas ou mieux utiliser des fibres optiques dont le diamètre peut être réduit au micron.
Un rayon lumineux chemine par réflexion totale à l'intérieur d'une fibre de verre entourée d'une gaine dont l'indice de réfraction est plus petit que celui du coeur de la fibre.
La fontaine lumineuse est illustrée dans la vidéo suivante :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Mesure des indices de réfraction
Les réfractomètres (type Abbe ou Pulfrich), qui sont destinés à mesurer des indices de réfraction, utilisent le phénomène de réfraction limite ou réflexion totale.
La substance d'indice inconnu x est mise au contact d'une substance d'indice élevé et connu N (N > x). Un dispositif approprié permet de mesurer l'angle limite λ. On en déduit alors : \(\mathrm x=\mathrm N~\sin\lambda\)
Les animations suivantes permettent d'illustrer le gradient d'indice, la réflexion partielle et totale (utilisation dans les réfractomètres) :