Focométrie

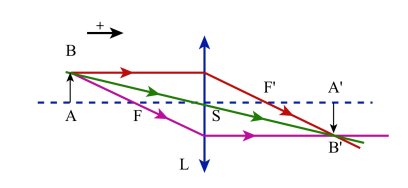
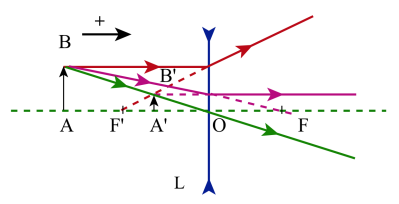
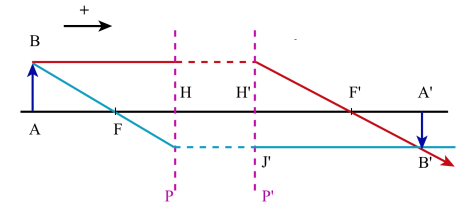
La distance focale^[1] d'une lentille mince^[2] quelconque peut se déduire des relations de conjugaison suivantes :

\(\frac1{\overline{SA'}}~-~\frac1{\overline{SA}}=\frac1{\overline{SF'}}=-\frac1{\overline{SF}}~\) ou \(~\overline{FA}~.~\overline{FA'}=-\overline{SF'}^2\)

On choisit comme sens positif le sens de propagation de la lumière incidente.

Les figures ci-contre rappellent la façon de construire l'image^[3] A'B' d'un objet^[4] AB pour une lentille convergente puis pour une lentille divergente.

Pour un système épais, en introduisant les points principaux H et H', les relations de conjugaison deviennent :

\(\frac1{\overline{H'A'}}~-~\frac1{\overline{HA}}=\frac1{\overline{H'F'}}=-\frac1{\overline{HF}}~\) ou \(~\overline{FA}~.~\overline{FA'}=\overline{H'F'}~.~\overline{HF}\)

Si les milieux extrêmes ne sont pas identiques et possèdent des indices différents n et n', les relations de conjugaison s'écrivent :

\(\frac{n'}{\overline{H'A'}}~-~\frac n{\overline{HA}}=\frac{n'}{\overline{H'F'}}=-\frac n{\overline{HF}}~\) ou \(~\frac{\overline{H'F'}}{\overline{H'A'}}~+~\frac{\overline{HF}}{\overline{HA}}=1\)