Mesure des rayons de courbure
applicable aux lentilles convergentes et divergentes
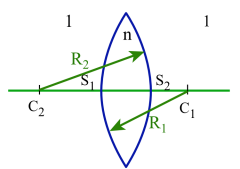
On peut également utiliser un sphéromètre pour mesurer les rayons de courbures \(R_{\mathit1}\) et \(R_{\mathit2}\) des faces de la lentille et connaissant l'indice n du verre de la lentille appliquer la relation :
\(\frac1{f'}=(n~-~1)\Big(\frac1{R_{\mathit1}}~-~\frac1{R_{\mathit2}}\Big)+\frac{(n~-~1)^2~e}{n.R_{\mathit1}.R_{\mathit2}}\)
avec :
n l'indice du verre de la lentille
\(\overline{S_{\mathit1}C_{\mathit1}}=R_{\mathit1}~\) et \(~\overline{S_{\mathit2}C_{\mathit2}}=R_{\mathit2}\)
les rayons de courbure des faces de la lentille
\(\overline{S_{\mathit1}S_{\mathit2}}=e\)
la distance qui sépare les sommets des faces d'entrée et de sortie de la lentille.
Remarque :
il faut que les lentilles soient suffisamment grandes pour pouvoir y poser le sphéromètre qui permettra la mesure des rayons de courbure
il est également nécessaire de connaître l'indice du verre de la lentille à la longueur d'onde de la lumière utilisée .