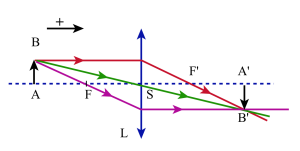
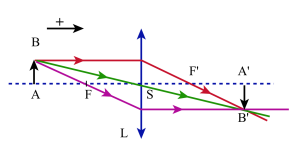
Méthode de Bessel et de Silbermann
applicable aux lentilles convergentes
Etablissons la relation qui existe entre la distance objet-image : \(~D=\overline{AA'}~\) et la position de l'objet \(~p=\overline{SA}\)
En appliquant la relation de conjugaison :
\(\frac1{\overline{SA'}}-\frac1{\overline{SA}}=\frac1{\overline{SF'}}\)
on en déduit : \(\overline{SA'}=\frac{\overline{SA}~.~\overline{SF'}}{\overline{SA}~+~\overline{SF'}}~\)
d'où \(~D=\overline{AA'}=\overline{AS}~+~\overline{SA'}=\frac{\overline{AS}~.~\overline{SA}}{\overline{SA}~+~\overline{SF'}}\)
soit : \(~D=-\frac{p^2}{p~+~f'}\)
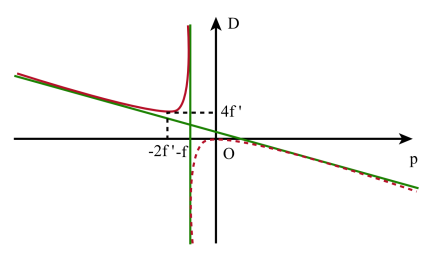
La fonction D = f ( p ) n'est pas définie pour p = - f ' et si \(~p~\;\to\;\pm\infty~\) alors \(~D~\;\to\;\pm\infty~\) la courbe est asymptote à la droite d'équation D = f ' - p
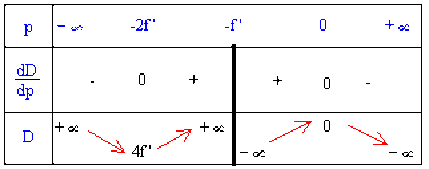
la dérivée vaut : \(\frac{dD}{dp}=-\frac{p~(p~+~2f')}{(p~+~f')^2}\)
étudions le signe de cette dérivée en fonction de p (voir tableau).
d'où la courbe représentative de D en fonction de p.
Pour une lentille convergente la partie de la courbe en pointillés rouge n'a pas de signification physique puisque l'objet[1] et son image[2] seraient virtuels.
Calculons les abscisses des points d'intersection \(p_{\mathit1}\) et \(p_{\mathit2}\) de la courbe D = f (p) avec la droite D = constante.
Elles sont solution de : \(~p^2~+~D.p~+~D.f'=0~\) les solutions sont donc :
\(p_{\mathit1}=\frac{-D~-~\sqrt{D~(D~-~4f')}}{2}\)
\(p_{\mathit2}=\frac{-D~+~\sqrt{D~(D~-~4f')}}{2}\)
à condition que \(D~(D~-~4f')\ge0~\) soit \(~D\ge4f'\)
Méthode de Bessel
si \(D>4f'\) on peut écrire :
\(D=\overline{AA'}=\overline{AS}~+~\overline{SA'}=p'-p\)
\(p'_{\mathit1}=p_{\mathit1}~+~D=\frac{-D~-~\sqrt{D~(D~-~4f')}}{2}~+~D=\frac{D~-~\sqrt{D~(D~-~4f')}}{2}=-p_{\mathit2}\)
\(p'_{\mathit2}=p_{\mathit2}~+~D=\frac{-D~+~\sqrt{D~(D~-~4f')}}{2}~+~D=\frac{D~+~\sqrt{D~(D~-~4f')}}{2}=-p_{\mathit1}\)
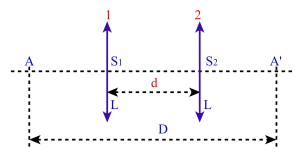
Etant donné une lentille convergente de distance focale[3] f ' et à condition que \(~D>4f'~\) il existe deux positions \(S_{\mathit1}\) et \(S_{\mathit2}\) pour lesquelles la lentille convergente donne en A' l'image nette d'un objet placé en A.
\(D=\overline{AA'}=\overline{AS_{\mathit1}}~+~\overline{S_{\mathit1}S_{\mathit2}}~+~\overline{S_{\mathit2}A'}=-p_{\mathit1}~+~d~+~p'_{\mathit2}\)
\(D=\overline{AA'}=\overline{AS_{\mathit2}}~+~\overline{S_{\mathit2}S_{\mathit1}}~+~\overline{S_{\mathit1}A'}=-p_{\mathit2}~-~d~+~p'_{\mathit1}\)
soit :
\(p'_{\mathit2}~-~p_{\mathit1}=D~-~d=-2p_{\mathit1}=D~+~\sqrt{D~(D~-~4f')}\)
\(p'_{\mathit1}~-~p_{\mathit2}=D~+~d=-2p_{\mathit2}=D~-~\sqrt{D~(D~-~4f')}\)
en multipliant membre à membre ces deux équations :
\((D~-~d)(D~+~d)=D^2~-~d^2=D^2-D~(D~-~4f')=D^2~-~D^2~+~4.D.f'=4.D.f'\)
on en déduit :
\(f'=\frac{D^2~-~d^2}{4D}\)
La méthode de Bessel pour déterminer la distance focale f ' consiste donc à s'imposer une distance D entre un objet A et un écran E et à rechercher les deux positions de la lentille L qui donnent une image nette de A sur l'écran E. En mesurant les distances D et d on calcule la valeur de la distance focale f '. S'il n'est pas possible de trouver ces deux positions on augmente la valeur de la distance D qui sépare l'objet A de l'écran E.
Méthode de Silbermann
Cette méthode est un cas particulier de la méthode de Bessel.
Si D = 4 f ' alors p = - 2 f ' et p' = 2 f '. L'image[2] et l'objet sont symétriques par rapport à S et le grandissement[4] vaut -1 : l'objet et son image sont situés dans les plans antiprincipaux.
On déduira donc la valeur de la distance focale f ' de la lentille en diminuant la distance D qui sépare l'objet de son image jusqu'à ce que l'image soit identique à l'objet mais renversée ; on divise alors la distance correspondante par 4 pour obtenir f '.
Simuler
L'animation didacticielle suivante illustre la détermination d'une distance focale par la méthode de Bessel et Silbermann :