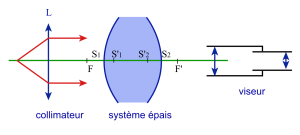
Méthode de Cornu
applicable aux systèmes épais
l'image[2] de la source, soit le foyer image[3] F ' et on repère la position du viseur soit : x (\(F '\)).
la face de sortie soit x (\(S_{\mathit2}\))
l'image de la face d'entrée soit x (\(S'_{\mathit2}\))
On en déduit :
\(\overline{F'S_{\mathit2}}=x(S_{\mathit2})~-~x(F')\)
\(\overline{F'S'_{\mathit1}}=x(S'_{\mathit1})~-~x(F')\)
On retourne alors le système épais face pour face et de la même manière que précédemment on mesure: x (\(F\)), x (\(S_{\mathit1}\)), x (\(S'_{\mathit1}\)). On en déduit alors :
\(\overline{FS_{\mathit1}}=x(S_{\mathit1})~-~x(F)\)
\(\overline{FS'_{\mathit2}}=x(S'_{\mathit2})~-~x(F)\)
Si l'on applique les relations de Newton à \(~S_{\mathit1}~\) ou \(~S_{\mathit2}~\) on obtient :
\(\overline{FS_{\mathit1}}~.~\overline{F'S'_{\mathit1}}=-f'^2\)
\(\overline{FS_{\mathit2}}~.~\overline{F'S'_{\mathit2}}=-f'^2\)
d'où la valeur de la distance focale[4] f '. On peut alors avec f ' déterminer la position des plans principaux correspondant à un grandissement[5] égal à 1 et réduire le système en ses éléments cardinaux.