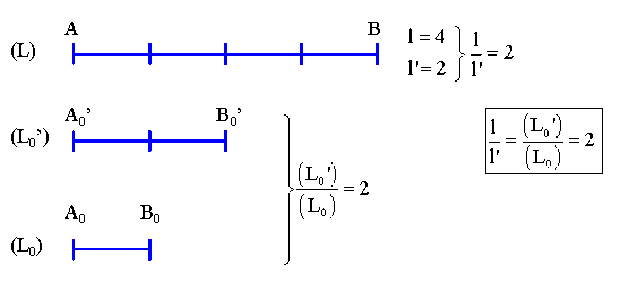Mesure d'une grandeur
Les observations faites des phénomènes naturels, sont utilisables, si nous pouvons associer un nombre à chaque état d'une grandeur.
Dans le cas où nous pouvons effectuer des opérations sur ces nombres (comparaison[1] et addition[2] de deux états de la grandeur avec les propriétés de commutativité et d'associativité) alors on peut donner un sens au rapport des nombres attachés aux deux états de la grandeur. Le passage de la notion de rapport à la notion de mesure s'effectue par la définition de la grandeur unité.
La mesure d'une grandeur \((G)\) est le nombre \(g\) qui exprime le rapport de cette grandeur à la grandeur \((G_0)\) de même espèce pris comme unité: \(g = \frac{(G)}{(G_{0})}\)
Soit \(l\) le nombre qui mesure la grandeur \((L)\) avec \((L_0)\) comme grandeur unité, alors par définition: \(l = \frac{(L)}{(L_{0})}\)
Exemple :
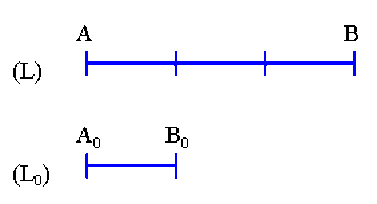
\(l = \frac{(L)}{(L_{0})}=3\)
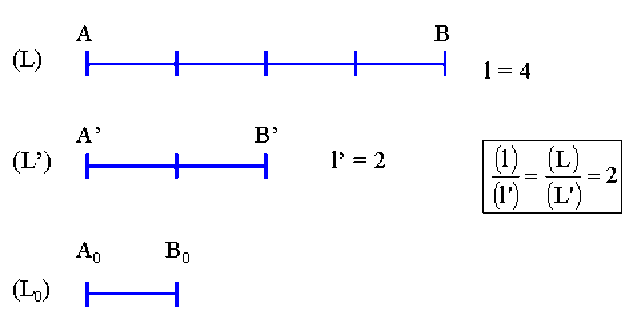
Si \(l\) et \(l'\) sont les deux nombres qui mesurent les grandeurs \((L)\) et \((L')\) avec la même unité \((L_0)\) alors :
\(l = \frac{(L)}{(L_{0})} ~\textrm{ et }~ l' = \frac{(L')}{(L_{0})} \Rightarrow \frac{(L)}{(L')} = \frac{l}{l'}\)
Définition :
Le rapport de deux grandeurs de même espèce est égal au quotient des nombres qui les mesurent avec la même unité.
Exemple :
Soit \(l\) et \(l'\) les nombres qui mesurent la même grandeur \((L)\) avec deux unités différentes \((L_0)\) et \((L_0')\) alors :
\(l = \frac{(L)}{(L_{0})} ~\textrm{ et } ~l' = \frac{(L)}{(L_{0}')} \Rightarrow \frac{(l)}{(l')} = \frac{(L_{0}')}{(L_{0})}\)
Définition :
Le rapport des nombres qui mesurent une même grandeur avec deux unités différentes est égal à l'inverse du rapport de ces unités.