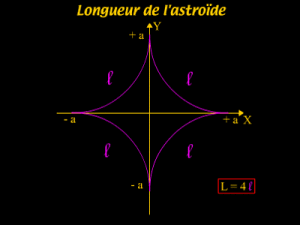
L'astroïde
Partie
Question
Aide simple
La symétrie de la figure, permet un calcul de la longueur du quart de la courbe.
Aide détaillée
L'équation de l'astroïde pour le 1er quadrant est de la forme :
\(y=+[(a^{2/3}-x^{2/3})]^{3/2}\) avec \(x\leq a\)
Solution simple
La longueur \(l\) d'un arc de courbe d'équation \(y = f(x)\) compris entre les points d'abscisse \(x = a\) et \(x = b\) est de la forme :
\(l=\int_a^b\sqrt{1+y'^2}dx\) avec \(y'=-\frac{(a^{2/3}-x^{2/3})^{1/2}}{x^{1/3}}\)
d'où \(L=4l=4\int_{x=0}^{x=a}a^{1/3}x^{-1/3}dx=6a\)
Solution détaillée
Par définition, la longueur \(l\) d'un arc de courbe d'équation \(y = f(x)\) compris entre les points d'abscisse \(x = a\) et \(x = b\) est de la forme :
\(l=\int_a^b\sqrt{1+y'^2}dx\)
La fonction \(y(x)\) admet pour fonction dérivée :
\(y'=\frac32(a^{2/3}-x^{2/3})^{1/2}(-\frac23x^{-1/3})=-\frac{(a^{2/3}-x^{2/3})^{1/2}}{x^{1/3}}\)
d'où pour l'arc de l'astroïde du 1er quadrant :
\(l=\int_0^a\sqrt{1+y'^2}dx=\int_0^a\sqrt{1+\frac{(a^{2/3}-x^{2/3})}{x^{2/3}}}dx=a^{1/3}\int_0^ax^{-1/3}dx=\frac32a\)
donc la longueur totale de l'astroïde sera \(L=4l=6a\)
Question
Aide simple
D'après la symétrie, calculer l'aire de la surface située dans le premier quadrant.
Aide détaillée
Pour le premier quadrant \(S=\int_0^ay(x)dx\) avec \(y=(a^{2/3}-x^{2/3})^{3/2}.\)Un changement de variable \(x=a\sin^3\theta\)conduit à l'expression \(\cos^4\theta\sin^2\theta\)qu'il faut linéariser avant intégration.
Solution simple
Par définition de l'aire :
\(S=\int_0^ay(x)dx=\int_0^a(a^{2/3}-x^{2/3})^{3/2}dx=3a^2\int_0^{\pi/2}\cos^4\theta\sin^2\theta d\theta\)
En Posant \(x=a\sin^3\theta.\) Après linéarisation de : \(\cos^4\theta\sin^2\theta=\frac1{16}(1+\frac12\cos2\theta-\cos4\theta-\frac12\cos6\theta)\)
Nous trouvons : \(S=\frac3{32}\pi a^2\) pour le quart de l'aire de l'astroïde d'où \(S_T=4S=\frac38\pi a^2\)
Solution détaillée
L'aire délimitée par l'astroïde d'équation \(y=[a^{2/3}-x^{2/3}]^{3/2}\)dans le premier quadrant est : \(S=\int_0^ay(x)dx=\int_0^a(a^{2/3}-x^{2/3})^{3/2}dx\)
Posons \(x=a\sin^3\theta\Leftrightarrow dx=3a\sin^2\theta\cos\theta d\theta\)
et
\(S=\int_0^{\frac{\pi}{2}}[a^{2/3}(1-\sin^2\theta)]^{3/2}3a\sin^2\theta\cos\theta d\theta=3a^2\int_0^{\frac{\pi}2}\cos^4\theta\sin^2\theta d\theta\)
Par linéarisation de \(\cos^4\theta\sin^2\theta\)nous obtenons
\(\cos^4\theta\sin^2\theta=\cos^2\theta\cos^2\theta\sin^2\theta=\frac{1+\cos2\theta}2\frac14\sin^22\theta=\frac14 \frac{1+\cos2\theta}2\frac{1-\cos4\theta}2\)
\(=\frac1{16}(1+\cos2\theta-\cos4\theta-\cos2\theta\cos4\theta)=\frac1{16}(1+\frac12\cos2\theta-\cos4\theta-\frac12\cos6\theta)\)
et
\(S=\frac{3a^2}{16}\int_0^{\frac{\pi}2}(1+\frac12\cos2\theta-\cos4\theta-\frac12\cos6\theta)d\theta=\frac{3a^2}{16}[\theta+\frac14\sin2\theta-\frac{\sin4\theta}4-\frac1{12}\sin6\theta]_0^{\frac{\pi}2}=\frac{3\pi a^2}{32}\)
pour la quart de l'astroïde , d'où la surface totale : \(S_T=4S=\frac{3\pi a^2}8\)
Question
Aide simple
D'après la symétrie de la courbe, l'arc du premier quadrant ,en rotation autour de \(Ox,\) balaye la moitié de la surface cherchée.
Aide détaillée
Par définition , l'élément d'aire \(dS\) balayée par l'arc du 1er quadrant est de la forme :
\(dS=2\pi y dl\) avec \(dl=\sqrt{1+y'^2}dx\)
Solution simple
L'aire de la surface de révolution sera : \(S_T=2S\) avec
\(S=2\pi\int_0^ay\sqrt{1+y'^2}dx=2\pi \int_0^a(a^{2/3}-x^{2/3})^{3/2}x^{-1/3}a^{1/3} dx=\frac 65 \pi a^2\) aprés intégration
d'où \(S_T=2S=\frac{12\pi a^2}5\)
Solution détaillée
L'aire engendrée par l'arc de courbe du 1er quadrant autour de l'axe des abscisses sera : \(S=2\pi\int_0^ay\sqrt{1+y'^2}dx\)
Sachant que \(y=(a^{2/3}-x^{2/3})^{3/2}\) et \(y'=-\frac{(a^{2/3}-x^{2/3})^{1/2}}{x^{1/3}}\)
nous obtenons pour \(\sqrt{1+y'^2}=\frac{a^{1/3}}{x^{1/3}}\)
d'où \(S=2\pi\int_0^a(a^{2/3}-x^{2/3})^{3/2}x^{-1/3}a^{1/3}dx\):
Intégrons en posant \(x=a\sin^3\alpha\Leftrightarrow dx=3a\sin^2\alpha \cos\alpha d \alpha\)
Alors : \((a^{2/3}-x^{2/3})^{3/2}x^{-1/3}a^{1/3}=3a^2\cos^4\alpha \sin\alpha\)
Et \(S=2\pi\int_0^{\pi/2}3a^2\cos^4\alpha \sin\alpha d\alpha\)
Aprés intégration, \(S=2\pi \times3a^2[-\frac{\cos^5\alpha}5]_0^{\frac{\pi}{2}}=\frac65\pi a^2\)
D'où pour la surface totale de révolution : \(S_T=2S=\frac{12\pi a^2}5\)
Question
Aide simple
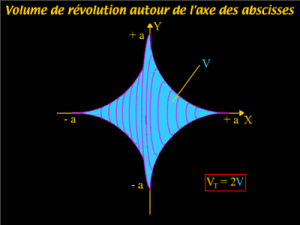
D'après la symétrie de la courbe, la surface de l'astroïde située dans le premier quadrant engendrera, lors de sa rotation autour de l'axe \(Ox,\) la moitié du volume cherché.
Aide détaillée
Par définition ,l'élément du volume \(dV\) balayée par l'élément de surface \(dS\) en rotation autour de \(Ox\) sera :
\(dV=\int dS=\int_0^a\pi y^2dx\)
Solution simple
Le volume engendré par la surface de l'astroïde située dans le premier quadrant en rotation autour de \(Ox\) sera :
\(V=\int_0^a\pi y^2dx=\int_0^a\pi(a^{2/3}-x^{2/3})^3dx=\frac{16}{105}\pi a ^3\)
D'où le volume total : \(V_T=2V=\frac{32\pi}{105}a^3\)
Solution détaillée
Le volume engendré par l'astroïde en rotation autour de \(Ox\) sera : \(V_T=2V\) avec
\(V=\int_0^a\pi y^2dx=\pi\int_0^a(a^{2/3}-x^{2/3})^3dx=\pi\int_0^a(a^2-3a^{4/3}x^{2/3}+3a^{2/3}x^{4/3}-x^2)dx\)
\(=\pi[a^2x-\frac95a^{4/3}x^{5/3}+\frac97a^{2/3}x^{7/3}-\frac13x^3]_0^a=\pi[a^3-\frac95a^3+\frac97a^3-\frac13a^3]=\frac{16\pi}{105}a^3\)
d'où le volume total :\(V_T=2V=\frac{32\pi}{105}a^3\)