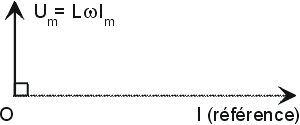Bobine
Démonstration :
Une bobine parcourue par un courant variable est traversée par un flux magnétique variable ; d'après la loi de Lenz, il y apparaît donc une f.é.m. s'opposant aux variations de flux :
\(e=-\frac{d\Phi}{dt}\)
Comme par définition de l'inductance \(L\) de la bobine : \(\Phi = L.i\), nous avons :
\(e=-L\frac{di}{dt}\)
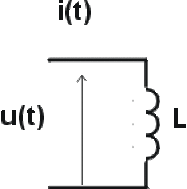
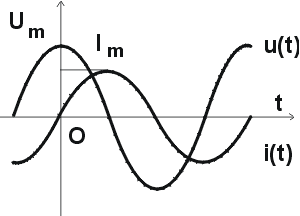
Si le courant variable parcourant la bobine a pour intensité \(i(t) = I_m \cos \omega t\), alors, comme avec la convention de signe choisie \(u = - e\) , il vient :
\(u(t) =L.\omega.I_m \sin \omega t = L.\omega.I_m \cos ( \omega t + \frac{\pi}{2})\)
or :
\(u(t) = U_m \cos ( \omega t +\varphi)\)
d'où les relations :
\(U_m =L.\omega.I_m ; \varphi = \frac{\pi}{2}\)
En notation complexe :
\(\underline i(t)=I_m\textrm{e}^{j\omega t}\)
\(\underline u(t)=L\frac{d\underline i}{dt}=j.L.\omega.I_m\textrm{e}^{j\omega t}=L.\omega.I_m\textrm{e}^{j\omega t}\textrm{e}^{j\frac{\pi}{2}}\)
comme : \(\underline u(t)=U_m\textrm{e}^{j(\omega t+\varphi)}=U_m\textrm{e}^{j\omega t}\textrm{e}^{j\varphi}\), nous avons les relations :
\(U_m = L.\omega.I_m ; \varphi = \frac{\pi}{2}\)