Condensateur
Explication :
Si on applique aux bornes d'un condensateur de capacité\(C\) une tension
\(u(t) = U_m \cos(\omega t +\varphi)\) , la charge de ce condensateur variera dans le temps avec pour équation :
\(q(t) = C.U_m \cos ( \omega t + \varphi)\)
D'où l'intensité du courant dans le circuit :
\(i(t)=\frac{dq}{dt}=-\omega.C.U_m\sin(\omega t+\varphi)=I_m\cos\omega t\)
En identifiant, on obtient :
\(U_m=\frac{I_m}{C.\omega} ;\;\varphi=-\frac{\pi}{2}\)
Le vecteur représentant la tension a donc une longueur proportionnelle à \(I_m/C.\omega\) et fait un angle de \(-\frac{\pi}{2}\) avec le vecteur représentant l'intensité, pris comme origine des phases.
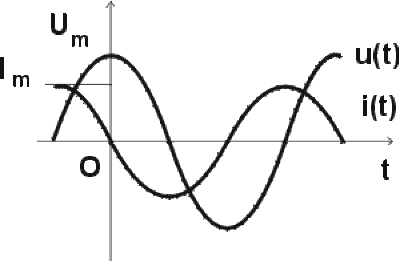
On dit aussi que la tension est en quadrature arrière par rapport au courant.
En notation complexe :
\(\underline u(t)=U_m\textrm{e}^{j(\omega t+\varphi)=U_m\textrm{e}^{j\omega t}\textrm{e}^{j\varphi}}\)
\(\underline q(t)=C.\underline u(t)=C.U_m\textrm{e}^{j\omega t}\textrm{e}^{j\varphi}\)
\(\begin{array}{lll}\underline i(t) & = & \frac{d\underline q}{dt}=C\frac{d\underline u}{dt}=j.\omega.CU_m\textrm{e}^{j\omega t}\textrm{e}^{j\varphi} \\ & = & \omega.CU_m\textrm{e}^{j\omega t}\textrm{e}^{j\frac{\pi}{2}}\end{array}\)
Comme : \(\underline i(t)=I_m\textrm{e}^{j\omega t}\)
nous avons les relations : \(U_m=\frac{I_m}{C.\omega} ;\;\varphi=-\frac{\pi}{2}\)
à \(t = 0\), le point complexe représentant la tension aux bornes d'un condensateur est un point de l'axe imaginaire.