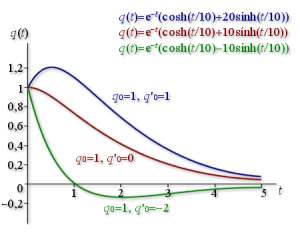
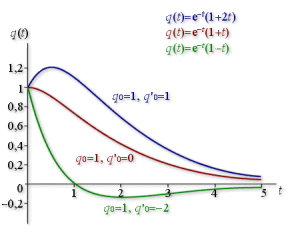
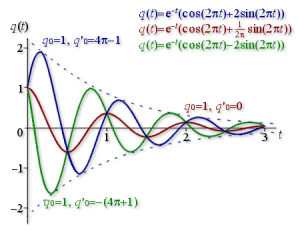
Etude de la forme de la réponse d'un oscillateur harmonique amorti en fonction des conditions initiales
Rappel :
Un oscillateur étant caractérisé par un coefficient d'amortissement \(\lambda\) et par une pulsation propre \(\omega_0\), le type de régime d'évolution se déduit du calcul du discriminant réduit : \(\Delta' = \lambda^2 - \omega_0^2\).
L'expression de la réponse \(q(t)\) d'un oscillateur donné dépend de deux constantes qui sont déterminées à partir des deux conditions initiales : q\((t = 0) = q_0\) et \(q'(t = 0) = q'_0\).
Connaissant \(\lambda\), \(\omega_0\), \(q_0\) et \(q'_0\), l'expression de la réponse \(q(t)\) de l'oscillateur est déterminée.
Les figures suivantes représentent les réponses de trois oscillateurs harmoniques amortis différents évoluant respectivement :
en régime apériodique pour le premier,
en régime critique pour le second,
en régime pseudo-périodique pour le troisième.
La réponse de chaque oscillateur est représentée successivement pour trois couples de valeurs des conditions initiales différents :
\((q_0 = 1, q'_0 = 0)\)
\((q_0 = 1, q'_0 > 0)\)
\((q_0 = 1, q'_0 < 0)\)
Pour chaque oscillateur, la condition \(q_0\) est fixe, la condition \(q'_0\) varie. Les valeurs numériques sont exprimées en unités \(\mathrm{ SI}\).
Les expressions des réponses sont données pour chaque figure.
Régime apériodique
Dans ce type de régime, \(q(t)\) tend vers 0 sans oscillation.
L'oscillateur est caractérisé par :
\(\lambda = 1 \mathrm{ rad.s}^{-1}\)
\(\omega_0 = 0,995 \mathrm{ rad . s}^{-1}\)
\(\Rightarrow \Delta' = \frac{1}{100} > 0\)
Régime critique
Dans ce type de régime, \(q(t)\) tend vers 0 sans oscillation.
L'oscillateur est caractérisé par :
\(\lambda = 1 \mathrm{ rad.s}^{-1}\)
\(\omega_0 = 1 \mathrm{ rad . s}^{-1}\)
\(\Rightarrow \Delta' = 0\)
Régime pseudo-périodique
L'oscillateur est caractérisé par :
\(\lambda = 1 \mathrm{ rad.s}^{-1}\)
\(\omega_0 = \sqrt{4 \pi^2 + 1} = 6,361 \mathrm{ rad.s}^{-1}\)
\(\Rightarrow \Delta' = \lambda^2 - \omega_0^2 = -\omega_1^2\)
\(\Rightarrow \Delta' = - 4 \pi^2 < 0\)
