Théorème des fonctions réciproques

Soit \(f\) une fonction continue strictement monotone sur un intervalle \(I.\) Alors

1) \(f(I)\) est un intervalle \(J\) de même nature que \(I\) (fermé, ouvert ou semi ouvert) et ses extrémités sont les limites de\( f\) aux extrémités de \(I.\)

2) La fonction \(f\) admet une fonction réciproque définie sur \(J = f(I)\); plus précisément, \(f\) définit une bijection de l'intervalle \(I\) sur l'intervalle \(J,\) donc il existe une fonction notée \(f^{-1}~\textrm{de}~J\) dans \(I,\) telle que

\(\begin{array} {|l|}\hline x \in I\\ y = f(x) \\ \hline \end{array}~~\Leftrightarrow~~\begin{array} {|l|}\hline y \in J\\ x = f^{-1}(y) \\ \hline \end{array}\)

3) La fonction réciproque \(f^{-1}\)est continue et strictement monotone sur \(J,\) de même sens de monotonie que \(f.\)

4) De plus, si \(f\) est dérivable en un point \(x_0\) de \(I\) et si \(f'(x_0)\)est non nul, \(f^{-1}\)est dérivable au point \(y_0 = f(x_0)~\textrm{et}~(f^{-1})'(y_0) = \frac{1}{f'(x_0)} = \frac{1}{f'(f^{-1}(y_0))}.\)

est vu dans la page précédente.

est une conséquence de ce qui précède :

L'image de l'intervalle \(I\) par la fonction continue \(f\) est un intervalle ; la fonction \(f\) étant strictement monotone sur \(I\) est injective, donc est une bijection de \(I\) sur \(J = f(I),\) donc il existe une application réciproque notée \(f^{-1},\) vérifiant

\(\forall x \in I,~~(f^{-1} \circ f)(x) = f^{-1}[f(x)] = id_I(x) = x~~et \\ \forall y \in J,~~(f \circ f^{-1})(y) = f[f^{-1}(y)] = id_J(y) = y\)

ce qui se résume bien par

\(\begin{array} {|l|}\hline x \in I\\ y = f(x) \\ \hline \end{array}~~\Leftrightarrow~~\begin{array} {|l|}\hline y \in J\\ x = f^{-1}(y) \\ \hline \end{array}\)

On se place dans le cas d'une fonction strictement croissante (La démonstration se fait facilement par analogie lorsque la fonction est strictement décroissante).

On démontre successivement les points suivants.

1. La fonction réciproque \(f^{-1}\)est strictement croissante sur \(J = f(I)\)

Soit \((y_1, y_2) \in J^2 \)tel que \(y_1 < y_2,\) et soient \(x_1 = f ^{-1}(y_1)~\textrm{et}~x_2 = f ^{-1}(y_2)\) ;

alors \(f(x_1) = y_1~\textrm{et}~f(x_2) = y_2\) Donc on a \(f(x_1) < f(x_2).\)

Donc \(x_1 < x_2\) (on ne peut pas avoir \(x_2 \leq x_1\)car cela entraînerait \(f(x_2) \leq f(x_1)\) puisque \(f\) est strictement croissante).

On a bien obtenu : \(\forall (y_1, y_2) \in J^2, y_1 < y_2 \Rightarrow f^{-1}(y_1) < f^{-1}(y_2).\)

2. La fonction réciproque \(f^{-1}\) est continue sur \(J.\)

Pour cela on démontre qu'elle est continue en tout point \(y_0\)appartenant à \(J.\)

Cela revient à démontrer que :

\(\forall \epsilon > 0, \exists \eta > 0, \forall y \in J, |y - y_0| < \eta \Rightarrow |f^{-1}(y) - f^{-1}(y_0)| < \epsilon\)

C'est-à-dire que, pour un réel strictement positif \(\epsilon\)donné, on cherche des conditions sur \(y\) pour que \(f^{-1}(y)\)appartienne à l'intervalle \(]f^{-1}(y_0) - \epsilon, f^{-1}(y_0) + \epsilon[.\)

On aimerait appliquer \(f\) aux extrémités de cet intervalle, mais il se peut que ces extrémités ne soient pas dans \(I.\) On est donc conduit à étudier les deux cas suivants :

• Le cas où \(f^{-1}(y_0)\)n'est pas une extrémité de \(I.\)

On veut montrer que \(f^{-1}\) est continue au point \(y_0,\) ce qui se traduit en langage mathématique par :

\(\forall \epsilon > 0, \exists \eta > 0, \forall y \in J, |y - y_0| < \eta \Rightarrow |f^{-1}(y) - f^{-1}(y_0)| < \epsilon\)

On pose \(f^{-1}(y_0) = x_0.\) Donc, pour un réel strictement positif \(\epsilon\)donné, on cherche des conditions sur \(y\) pour que \(|f^{-1}(y) - x _0| < \epsilon,\) c'est-à-dire pour que \(f^{-1}(y)\)appartienne à l'intervalle \(]x_0 - \epsilon, x_0 + \epsilon[.\)

On est dans le cas où \(f^{-1}(y_0) = x_0\)n'est pas une extrémité de \(I.\)

Comme \(I\) est un intervalle, il existe un

réel \(\alpha, \alpha > 0~\textrm{et}~\alpha < \epsilon\) tel que

l'intervalle \([x_0 - \alpha, x_0 + \alpha]\)soit contenu dans \(I.\)

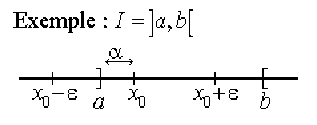
Soit \(y_1 = f(x_0 - \alpha)~\textrm{et}~y_2=f(x_0 + \alpha)\) ; comme \(f\) est croissante on a \(y_1 < y_0 < y_2\) car \(y_0 = f(x_0)\);

soit alors \(\eta = min(y_0 - y_1, y_2 - y_0)\);

cela entraîne : \(y_1 \leq y_0 - \eta < y_0 + \eta \leq y_2.\)

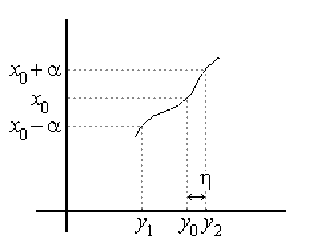
Donc pour tout \(y\) vérifiant \(|y - y_0| < n,\) on a \(y_0 - \eta < y < y_0 + \eta,\) donc \(y_1 < y < y_2,\) donc \(y \in J,\) car \(J\) est un intervalle.

D'où \(f^{-1}(y_1) < f^{-1}(y) < f^{-1}(y_2)\) car \(f^{-1}\)est strictement croissante, c'est-à-dire, d'après la définition de \(y_1\)et de \(y_2\):

\(x_0 - \alpha < f^{-1}(y) < x_0 + \alpha\)et comme \(x_0 = f^{-1}(y_0),\)

\(f^{-1}(y_0) - \alpha < f^{-1}(y) < f^{-1}(y_0) + \alpha,\) d'où \(|f^{-1}(y) - f^{-1}(y_0)| < \alpha\)

et puisqu'on a choisi \(\alpha \leq \epsilon,\) on obtient \(|f^{-1}(y) - f^{-1}(y_0)| < \epsilon.\)

On a donc démontré la proposition suivante :

\(\forall \epsilon > 0, \exists \eta > 0, \forall y \in J, |y - y_0| < \eta \Rightarrow |f^{-1}(y) - f^{-1}(y_0)| < \epsilon\)

La fonction réciproque \(f^{-1}\)est bien continue en \(y_0.\)

• Le cas où \(f^{-1}(y_0)\)est une extrémité de \(I.\)

On veut montrer que \(f^{-1}\)est continue au point \(y_0,\) ce qui se traduit en langage mathématique par :

\(\forall \epsilon > 0, \exists \eta > 0, \forall y \in J, |y - y_0| < \eta \Rightarrow |f^{-1}(y) - f^{-1}(y_0)| < \epsilon\)

On pose \(f^{-1}(y_0) = x_0.\) Donc, pour un réel strictement positif \(\epsilon\)donné, on cherche des conditions sur \(y\) pour que \(|f^{-1}(y) - x_0| < \epsilon,\) c'est-à-dire pour que \(f^{-1}(y)\)appartienne à l'intervalle \(]x_0 - \epsilon, x_0 +\epsilon[.\)

On est dans le cas où \(f^{-1}(y_0) = x_0\)est une extrémité de \(I\) ; on fait la démonstration en supposant que \(x_0\)est la plus petite extrémité de \(I\) (on sait alors que \(y_0\)est la plus petite extrémité de \(J\)).

Alors il existe un réel \(\alpha, \alpha > 0~\textrm{et}~ \alpha \leq \epsilon\) tel que \([x_0, x_0 + \alpha]\)soitcontenu dans \(I\) (on rappelle que \(I\) est non vide et non réduit à un point).

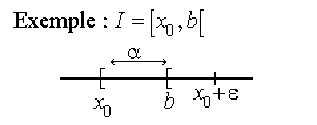
Soit \(y_1 = f(x_0 + \alpha)\); donc \(y_0 < y_1\)car \(y_0 = f(x_0)\)est la plus petite extrémité de \(J\) (ou parce que \(f\) est croissante). Soit alors \(\eta = y_1 - y_0.\)

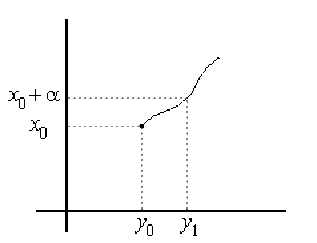
Donc pour tout \(y, y \in J,\) vérifiant \(|y - y_0| < \eta,\) on a \(y_0 < y < y_0 + \eta,\) donc \(y_0 < y < y_1,\) d'où \(f^{-1}(y_0) < f^{-1}(y) < f^{-1}(y_1),\) car \(f^{-1}\)est strictement croissante, c'est-à-dire d'après la définition de \(y_1, x_0 < f^{-1}(y) < x_0 + \alpha\) et comme \(x_0 = f^{-1}(y_0), f^{-1}(y_0) < f^{-1}(y) < f^{-1}(y_0) + \alpha,\) d'où \(|f^{-1}(y) - f^{-1}(y_0)| < \alpha\) et puisqu'on a choisi \(\alpha \leq \epsilon,\) on obtient \(|f^{-1}(y) - f^{-1}(y_0)| < \epsilon.\)

On a donc démontré la proposition suivante :

\(\forall \epsilon > 0, \exists \eta > 0, \forall y \in J, |y - y_0| < \eta \Rightarrow |f^{-1}(y) - f^{-1}(y_0)| < \epsilon\)

La fonction réciproque \(f^{-1}\) est bien continue en \(y_0.\)

On suppose \(f\) dérivable en un point\(x_0~\textrm{de}~I,~\textrm{et}~f'(x_0)\) et non nul.

On montre que \(f^{-1}\)est dérivable au point \(y_0 = f(x_0)\)et que \((f^{-1})'(y_0) = \frac{1}{f'(x_0)}.\)

Pour cela on montre que le rapport \(\frac{f^{-1}(y) - f^{-1}(y_0)}{y - y_0}\)a une limite lorsque \(y\) tend vers \(y_0\)et que cette limite est \(\frac{1}{f'(x_0)}.\)

Soit \(x = f^{-1}(y)\); on a \(x_0 = f^{-1}(y_0)\)et par conséquent \(\frac{f^{-1}(y) - f^{-1}(y_0)}{y - y_0} = \frac{x - x_0}{f(x) - f(x_0)}.\)

Or \(f^{-1}\)est continue, donc quand \(y\) tend vers \(y_0, x = f^{-1}(y)\) tend vers \(x_0 = f^{-1}(y_0)\)et le rapport \(\frac{x - x_0}{f(x) - f(x_0)}\)a une limite puisque \(f\) est dérivable en \(x_0\)et que sa dérivée \(f'(x_0)\)est non nulle. Cette limite est bien égale à \(\frac{1}{f'(x_0)}.\)