Exemple
On considère la fonction numérique \(f\) définie sur \(I=[0, \sqrt{2}[~\textrm{par}~ x \mapsto f(x) = \frac{x^3}{4 - x^4}\)
La fonction \(f\) est le quotient des deux fonctions \(g~\textrm{et}~h\) définies sur \(I\) par \(x \mapsto g(x) = x^3~\textrm{et}~x \mapsto h(x) = 4 - x^4.\)
Les fonctions \(g~\textrm{et}~h\) sont continues sur \(I~\textrm{et}~h\) ne s'annule pas sur \(I,\) on en déduit que \(f\) est continue sur \(I.\)
Sur \(I,\) la fonction \(g\) est strictement croissante et positive, la fonction \(h\) est strictement décroissante et positve, donc la fonction \(\frac{1}{h}\) est strictement croissante et positive, donc \(f\) est strictement croissante comme produit de deux fonctions strictement croissantes positives.
Comme la fonction \(f\) satisfait aux hypothèses du théorème des fonctions réciproques, on a les résultats suivants :
\(f([0, \sqrt{2}[) = [f(0),\displaystyle \lim_{x \rightarrow \sqrt{2}}f(x)[~\textrm{d'où}~f([0,\sqrt{2}[) = [0, +\infty[.\)
La fonction \(f\) admet une fonction réciproque, notée \(f^{-1},\) définie sur \(J = [0, \infty[.\)
On ne sait pas expliciter la fonction \(f^{-1}\)mais on sait que :
La fonction \(f^{-1}\) est continue sur \(J = [0, +\infty[,\)
la fonction \(f^{-1}\) est strictement croissante sur \(J\)
\(f^{-1}([0, +\infty[) = [0, \sqrt{2}[~\textrm{avec}~f^{-1}(0) = 0~\textrm{et}~lim_{x \rightarrow +\infty}f^{-1}(x) = \sqrt{2}\)
De plus les fonctions \(g~\textrm{et}~h\) étant dérivables sur \(I,~f\) est dérivable comme quotient de deux fonctions dérivables, la fonction du dénominateur ne s'annulant pas sur \(I.\) Sa dérivée, après calculs, est la fonction \(f' : x \mapsto \frac{x^2(12 + x^4)}{(4 - x^2)^2}.\)
D'après le théorème des fonctions réciproques, la fonction \(f^{-1}\)est dérivable en tout point image d'un \(x\) tel que \(f'(x) \neq 0.\)
Mais on a : \(f'(x) = 0 \Leftrightarrow x = 0,\) donc \(f^{-1}\)est dérivable en tout point autre que \(f(0).\)
Donc \(f^{-1}\)est dérivable sur \(]0, +\infty[~\textrm{et}~\forall a \in ]0, +\infty[, (f^{-1})'(a) = \frac{1}{f'(f^{-1}(a))}.\)
Par exemple, \(f\) est définie en 1 et \(f(1) = \frac{1}{3},\) donc \(f^{-1}\)est dérivable en \(\frac{1}{3}~\textrm{et}~(f^{-1})'(\frac{1}{3}) = \frac{1}{f'(1)} = \frac{9}{13}\)
Représentation graphique de \(f\) et de \(f^{-1}\)dans un repère orthonormé.
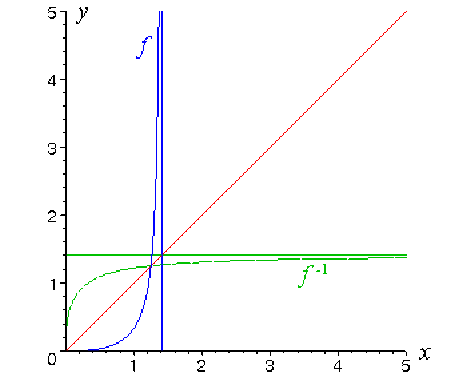
Remarques sur la représentation graphique de \(f\) et de \(f^{-1}.\)
Comme \(f(0)~\textrm{et}~f'(0) = 0,\) la tangente à l'origine de la courbe représentative de \(f\) est horizontale.
On en déduit que la tangente à l'origine de la courbe représentative de \(f^{-1}\)est verticale, puisque les deux courbes sont symétriques par rapport à la première bissectrice.
Comme \(lim_{x \rightarrow \sqrt{2}}f(x) = +\infty\) et comme \(lim_{x \rightarrow +\infty}f^{-1}(x) = \sqrt{2},\) la droite \(x = \sqrt{2}\) est asymptote à la courbe représentative de \(f,\) tandis que la droite \(y = \sqrt{2}\)est asymptote à la courbe représentative de \(f^{-1}.\)