Action des transformations élémentaires sur la matrice unité
Echange de lignes ou de colonnes
La question est la suivante : quelle matrice obtient-on lorsque l'on permute les lignes\( \mathcal L_i\) et\( \mathcal L_j\) \((1\leq i\leq n,1\leq j\leq n\) et \(i\neq j)\) de la matrice unité \(\mathcal I_n\)?
La matrice obtenue a les propriétés suivantes :
Les coefficients de la \(i\)-ième ligne et \(i\)-ième colonne et de la \(j\)-ième ligne et jème colonne de la matrice obtenue sont nuls.
Les coefficients de la \(i\)-ième ligne et \(j\)-ième colonne et\( j\)-ième ligne et\( i\)-ième colonne sont égaux à \(1\).
Les autres coefficients de la diagonale principale sont inchangés donc égaux à \(1\) et tous les autres coefficients (inchangés eux aussi) sont nuls.
On trouve donc la matrice
Notation : Cette matrice est notée et on l'appelle, dans ce cours, matrice d'échange.
Attention :
il y a une ambiguïté dans la notation puisque l'ordre de la matrice n'est pas indiqué. En fait la considération du contexte permettra de le déterminer sans problèmes.
Par exemple, si \(n=5,i=2,j=4\) on a
\(\displaystyle{\Delta_{2,4}=\left(\begin{array}{cccccc}1&0&0&0&0\\0&0&0&1&0\\0&0&1&0&0\\0&1&0&0&0\\0&0&0&0&1\end{array}\right)}\)
Il est immédiat que l'échange des colonnes \(\mathcal C_i\) et \(\mathcal C_j\) \((1\leq i\leq n,1\leq i\leq n\) et \(i\neq j)\) de la matrice unité \(\mathcal I_n\) conduit à la même matrice.
Proposition : Propriétés des matrices du type \Delta_{i,j}
Soit\( n\) un entier supérieur ou égal à \(2\). Pour tout entiers \(i\) et \(j\) \((1\leq i\leq n,1\leq i\leq n\) et \(i\neq j)\), la matrice \(\Delta_{i,j}\) est une matrice symétrique, c'est-à-dire telle que \({}^t\Delta_{i,j}=\Delta_{i,j}\) et vérifie la propriété :\( \Delta_{i,j}=\Delta_{i,j}\).
Ces résultats sont immédiats, à partir de la formule explicite de \(\Delta_{i,j}\).
Multiplication de chaque élément de la i-ième ligne (respectivement la i-ième colonne) par un coefficient \lambda non nul
Toujours la même question : quelle matrice obtient-on lorsque l'on multiplie la ligne \(\L_i\) (\(1\leq i\leq n\)) de la matrice unité \(\mathcal I_n\) par un coefficient \(\lambda\) non nul ?
La matrice obtenue est diagonale, l'élément de la i-ième ligne et i-ième colonne est égal à\( \lambda\), les autres éléments de la diagonale principale, inchangés, sont égaux à \(1\).
On trouve donc la matrice \(\displaystyle{\left(\begin{array}{cccccc}1&0&\cdots&\cdots&0\\0&\ddots&&&\vdots\\\vdots&&\lambda&&\vdots\\\vdots&&&\ddots&0\\0&\cdots&\cdots&0&1\end{array}\right)}\)
Le résultat est évidemment le même si on multiplie la i-ième colonne par le scalaire \(\alpha\).
Notation : Cette matrice est notée \(\mathcal D(\alpha)\) et est souvent appelée matrice de dilatation.
Exemple : \(\mathcal D_2(\alpha)=\left(\begin{array}{cccccc}1&0&0\\0&\lambda&0\\0&0&1\end{array}\right)\)
Addition aux éléments de la i-ième ligne \mathcal L_i de \mathcal I_n (respectivement de la i-ième colonne de \mathcal C_i de \mathcal I_n ) de \alpha fois les éléments correspondants de la j-ième ligne \mathcal L_j de \mathcal I_n (respectivement la j-ième colonne de \mathcal I_n )
On suppose que \(1\leq i\leq n,1\leq j\leq n \)et\( i\neq j\).
En modifiant les lignes de \(\mathcal I_n\), il est clair que la matrice obtenue est la matrice triangulaire appartenant à \(\mathcal M_n(\mathbf K)\) telle que :
Les éléments de la diagonale principale sont tous égaux à \(1\)
Le scalaire \(\lambda\) se trouve à la i-ième ligne et j-ième colonne
Tous les autres éléments sont nuls.
On obtient donc, par la transformation \(\mathcal H_{i,j}(\lambda)\) appliquée à \(\mathcal I_n\), la matrice
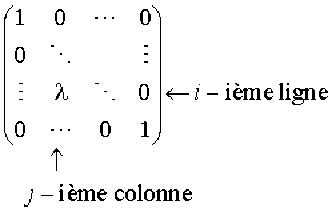
De même, la transformation élémentaire \(\mathcal K_{j,i}(\lambda)\) appliquée à \(\mathcal I_n\) modifie les colonnes : on obtient une matrice de même type mais où l'élément \(\lambda\) se trouve à la j-ième ligne et i-ième colonne.
Notation : on note \(\mathcal T_{i,j}(\lambda)\in\mathcal M_n({\mathbf K})\) la matrice :
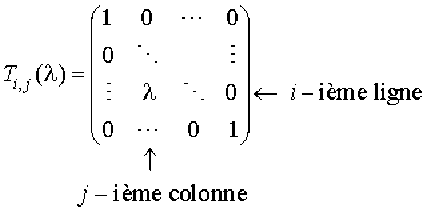
Les matrices de ce type sont souvent appelées matrices de transvection.
Exemple :
\(\mathcal T_{1,3}(-1)=\left(\begin{array}{cccccc}1&0&-1\\0&1&0\\0&0&1\end{array}\right)\)
Ces deux types de matrices, dilatation et transvection, sont appelées matrices élémentaires. En résumé, on a la définition suivante...