Multiplication à droite par une matrice élémentaire ou une matrice d'échange et opérations élémentaires sur les colonnes
Théorème : Opérations élémentaires sur les colonnes
Soit \(n\) et \(p\) deux entiers supérieurs ou égaux à \(2\). Soit \(\mathcal M\in\mathcal M_{n,p}(\mathbf K)\) .
Soient\( i\) et \(j\) deux entiers distincts compris entre \(1\) et \(p\) et un élément quelconque de \(\mathbf K\). On considère la matrice d'ordre \(p\), \(\mathcal T_{i,j}(\lambda)\).
La matrice produit \(\mathcal M\mathcal T_{i,j}(\lambda)\) s'obtient en remplaçant la j-ième colonne \(\mathcal C_j\) de \(\mathcal M\) par\( \mathcal C_j+\lambda\mathcal C_i\) , et en laissant les autres inchangées.
Soient \(i\) un entier compris entre \(1\) et \(p\) et un élément non nul de \(\mathbf K\). On considère la matrice d'ordre \(p\),\( \mathcal D_i(\lambda)\). La matrice produit \(\mathcal M\mathcal D_i(\lambda)\) s'obtient en remplaçant la i-ième colonne \(\mathcal C_i\) de \(\mathcal M\) par \(\lambda\mathcal C_i\), et en laissant les autres inchangées.
Soient\( i\) un entier compris entre \(1\) et \(p\). On considère la matrice d'ordre \(p,\Delta_{i,j}\) . La matrice produit \(\mathcal M\Delta_{i,j}\) s'obtient en échangeant les i-ième et j-ième colonnes de \(\mathcal M\), et en laissant les autres inchangées.
Remarque :
Attention, à l'ordre des indices dans le premier cas. Le produit à droite par la matrice élémentaire \(\mathcal T_{i,j}(\lambda)\), où j est le deuxième indice donne une transformation de la j-ième colonne de \(\mathcal M\).
La preuve de ces formules est basée sur les expressions des matrices et des matrices élémentaires en fonction des matrices \(E_{i,j}\).
Démonstration :
Soit \(\mathcal M=(a_{k,l})\) une matrice appartenant à \(\mathcal M_{n,p}(\mathbf K)\). Soient\( i \)et \(j\) deux entiers distincts, compris entre \(1\) et\( p\).
Soit la matrice carrée d'ordre p, \(\mathcal T_{i,j}(\lambda)\) le produit \(\mathcal M\mathcal T_{i,j}(\lambda)\) existe. C'est une matrice à \(n\) lignes et \(p\) colonnes, donc du même type que \(\mathcal M\).
La matrice \(\mathcal T_{i,j}(\lambda)\) peut s'écrire \(\mathcal T_{i,j}(\lambda)=\mathcal I_p+\lambda E_{i,j}\) (où \(E_{i,j}\) est carrée d'ordre \(p\)), d'où
\(\displaystyle{\mathcal M\mathcal T_{i,j}(\lambda)=\mathcal M(\mathcal I_p+\lambda E_{i,j}=\mathcal M+\lambda\mathcal ME_{i,j}}\)
Pour conclure, il s'agit de calculer la matrice \(\mathcal ME_{i,j}\).
On a \(\displaystyle{\mathcal ME_{i,j}=(\sum_{\begin{array}{cccccc}1\leq k\leq n\\1\leq l\leq p\end{array}}a_{k,l}E_{k,l})E_{i,j}=\sum_{\begin{array}{cccccc}1\leq k\leq n\\1\leq l\leq p\end{array}}a_{k,l}(E_{k,l}E_{i,j})}\)
Compte tenu des règles de multiplication des matrices de type\( E_{r,s}\),
il vient \(\displaystyle{\mathcal ME_{i,j}=\sum_{\begin{array}{cccccc}1\leq k\leq n\\1\leq l\leq p\end{array}}a_{k,l}E_{k,l}}\)
Donc\( \displaystyle{\mathcal M\mathcal T_{i,j}(\lambda)=\mathcal M+\lambda\sum_{1\leq k\leq n}a_{k,j}E_{k,j}}\)
Interprétation de cette égalité :
On a :
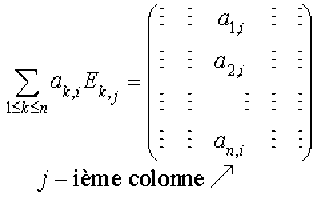
Les colonnes, autres que la j-ième, ne sont composées que de zéros.
Alors, la j-ième colonne de la matrice\( \mathcal M\mathcal T_{i,j}(\lambda)\) est obtenue en ajoutant\( \lambda\) fois sa i-ième colonne à la j-ième colonne de la matrice \(\mathcal M\) et en ne modifiant pas les autres. C'est le résultat voulu.
Remarque sur les notations : Attention
Dans la formule \(\displaystyle{\mathcal ME_{i,j}=(\sum_{\begin{array}{cccccc}1\leq k\leq n\\1\leq l\leq p\end{array}}a_{k,l}E_{k,l})E_{i,j}}\) , les matrices de type \(E_{r,s}\) qui interviennent ne sont pas toutes de même type, ce que les notations ne mettent pas en évidence. En effet, celles qui interviennent dans l'expression de \(\mathcal M\), soit \(\displaystyle{\mathcal M=\sum_{\begin{array}{cccccc}1\leq k\leq n\\1\leq l\leq p\end{array}}a_{k,l}E_{k,l}}\), sont de même type que \(\mathcal M\), soit à \(n\) lignes et \(p\) colonnes.
Par contre la matrice\( E_{i,j}\) de l'expression \(\mathcal ME_{i,j}\) est carrée d'ordre \(p\) puisqu'elle provient de la définition de la matrice carrée d'ordre \(p\),\(\mathcal T_{i,j}(\lambda)\) .
Le produit indiqué existe et donne une matrice à \(n\) lignes et \(p\) colonnes.
L'ambiguïté apparente des notations n'est donc pas gênante, à condition de bien réfléchir au contexte.
- Soit \(i\) un entier compris entre \(1\) et \(p\) et la matrice d'ordre \(p,\mathcal D_i(\lambda)\)
\(\displaystyle{\mathcal D_i(\lambda)=\left(\begin{array}{cccccc}1&&&&\\&\ddots&&&\\&&\lambda&&\\&&&\ddots&\\&&&&1\end{array}\right)=\lambda E_{i,i}+\sum^{j=p}_{\begin{array}{cccccc}j=1\\ j\neq1\end{array}}E_{j,j}}\)
Alors \(\displaystyle{\mathcal M\mathcal D_{i}(\lambda)=(\sum_{\begin{array}{cccccc}1\leq k\leq n\\1\leq l\leq p\end{array}}a_{k,l}E_{k,l})(\lambda E_{i,i}+\sum^{j=p}_{\begin{array}{cccccc}j=1\\ j\neq1\end{array}}E_{j,j})}\)
soit \(\displaystyle{\mathcal M\mathcal D_i{\lambda}=\sum_{\begin{array}{cccccc}1\leq k\leq n\\1\leq l\leq p\end{array}}a_{k,l}E_{k,l}+\lambda\sum_{1\leq k\leq n}a_{k,j}E_{k,j}}\)
Cette matrice est obtenue à partir de la matrice \(\mathcal M\) en multipliant la i-ième colonne par \(\lambda\) et en laissant les autres inchangées.
Remarque :
même remarque que précédemment pour les notations.
Le calcul de \(\mathcal M\mathcal D_i(\lambda)\), peut aussi être fait sans difficultés, directement, avec les formules du produit de deux matrices.
- Soit\( i \textrm{ et }j\) deux entiers compris entre \(1\) et \(p\) et \(\Delta_{i,j}\) la matrice d'échange.
\(\displaystyle{\mathcal M\Delta_{i,j}=(\sum_{\begin{array}{cccccc}1\leq k\leq n\\1\leq l\leq p\end{array}}a_{k,l}E_{k,l})(E_{i,j}+E_{j,i}+\sum_{\begin{array}{cccccc}1\leq s\leq p\\s\neq i\\s\neq j\end{array}}E_{s,s})}\)
Compte tenu de la table de multiplication des matrices \(E_{t,q}\),
on obtient \(\displaystyle{\mathcal M\Delta_{i,j}=\Bigg(\sum_{\begin{array}{cccccc}1\leq k\leq n\\1\leq l\leq p\end{array}}a_{k,l}E_{k,l}E_{i,j}+\sum_{\begin{array}{cccccc}1\leq k\leq n\\1\leq l\leq p\end{array}}a_{k,l}E_{k,l}E_{j,i}+\bigg(\sum_{\begin{array}{cccccc}1\leq k\leq n\\1\leq l\leq p\end{array}}a_{k,l}E_{k,l}\bigg)\bigg(\sum_{\begin{array}{cccccc}1\leq s\leq p\\s\neq i\\s\neq j\end{array}}E_{s,s}\bigg)\Bigg)}\), d'où \(\displaystyle{\mathcal M\Delta_{i,j}=\sum_{\begin{array}{cccccc}1\leq k\leq n\end{array}}a_{k,i}E_{k,j}\sum_{1\leq k\leq n}a_{k,j}E_{k,i}+\sum_{\begin{array}{cccccc}1\leq k\leq n\\1\leq l\leq p\\l\neq i\\l\neq j\end{array}}a_{k,l}E_{k,l})}\)
Interprétation de ce résultat : la j-ième colonne de la matrice \(\mathcal M\Delta_{i,j}\) est donnée par le premier terme de cette somme : ses coefficients sont ceux de la i-ième colonne de \(\mathcal M\). De même les coefficients de la i-ième colonne de \(\mathcal M\Delta_{i,j}\) sont ceux de la j-ième colonne de \(\mathcal M\) (deuxième terme de la formule). Enfin les autres colonnes de \(\mathcal M\Delta_{i,j}\) sont égales aux colonnes correspondantes de\( \mathcal M\) (dernier terme de la formule).
Remarque : Remarque importante :
Il en résulte que la multiplication à droite par un produit \(\displaystyle{\prod^{i=k}_{i=1,i\neq j}\mathcal T_{i,j}(\lambda_i)}\) de matrices élémentaires (de type transvection) ayant le même indice j correspond à une transformation des colonnes : on obtient une matrice dont la j-ième colonne est égale à \(\displaystyle{\mathcal C_j+\sum_{i=1,i\neq j}^{i=k}\lambda_i\mathcal C_i}\).
En particulier si \(\mathcal C_i\) est combinaison linéaire de colonnes \(\mathcal C_i\), il existe un produit de matrices élémentaires tel que, en multipliant la matrice à droite par ce produit, on obtienne une matrice dont la j-ième colonne est une colonne formée uniquement de \(0\).
Ce résultat sera très utile dans la suite.