Exercice 17
Partie
Question
Étudier la convergence uniforme de la suite de fonctions (\(f_n\)) définies sur \(\mathbb{R^+}\) par :
\(f_n(x) = \frac{x^2}{1 + nx^2}\)
Aide simple
La suite (\(f_n\)) converge simplement sur \(\mathbb{R^+}\) vers \(\tilde{0}\).
Pour avoir convergence uniforme, il faut montrer que \(\underset{x \in l}{sup} \Big \{ |f_n(x )- f(x) | \Big \} \) tend vers 0 quand n \(\rightarrow +\infty\) . Il faut donc exprimer ce sup (ou un majorant) en fonction de n et regarder s'il tend vers 0 quand n tend vers \(+\infty\) .
Solution détaillée
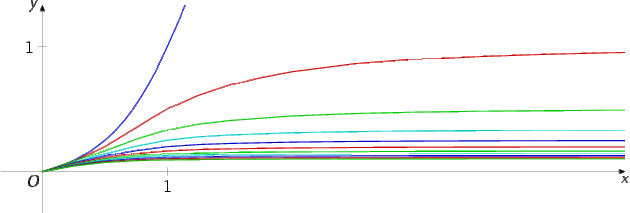
On cherche \(\underset{x \in \mathbb{R_+}}{sup} \Big \{ |f_n(x )- 0 | \Big \} \) .
Pour tout n, \(| f_n(x)- 0 |= | f_n(x) |= f_n(x) = \frac{x^2}{1 + nx^2}\)
\(f_n'(x) = \frac{2x}{(1 + nx^2)^2} \geqslant 0\) et \(f_n'(x)\) ne s'annule que pour x = 0.
La fonction \(f_n\) est donc strictement croissante sur \(\mathbb{R_+}\).
\(\displaystyle \lim_{x \rightarrow +\infty \textrm{ }} f_n(x) = \frac{1}{n}\) (pour n \(\geqslant\) 1).
Donc \(\underset{x \in \mathbb{R_+}}{sup} \Big \{ |f_n(x )- 0 | \Big \} = \frac{1}{n}\)
Comme cette borne supérieure tend vers 0 lorsque n tend vers \(+\infty\), on en déduit, par définition, que la suite (\(f_n\)) converge uniformément sur \(\mathbb{R_+}\) vers \(\tilde{0}\) .
La suite (\(f_n\)) converge uniformément sur \(\mathbb{R_+}\) vers \(\tilde{0}\) .