Potentiel : distribution continue /Potentiel créé par un anneau chargé 1/1
Partie
Question
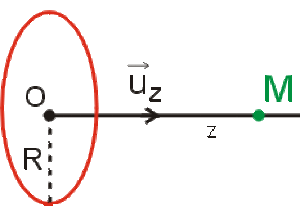
Soit un anneau de centre \(O\) et de rayon \(R\) chargé uniformément d'une densité linéique de charges \(\lambda\). Sachant que le champ \(\vec E\) existant en un point \(M\) de l'axe à la distance \(z\) de \(O\) est :
\(\vec E = \frac{\lambda R}{2 \epsilon_0} \frac{z}{\Big( R^2 + z^2 \Big)^{\frac 3 2}} \vec u_z\) ,
déduire le potentiel \(V\) en ce point \(M\).
Aide simple
\(\displaystyle{V(A) - V(B) = - \int_B^A \vec E . \mathrm d \vec M}\)
L' origine des potentiels peut être prise à l'infini puisque la source est localisée \(V(B) = V(\infty) = 0\)
\(\displaystyle{V(M) = - \int_{\infty}^M \vec E . \mathrm d \vec M}\)
Aide détaillée
\(\displaystyle{V(M) = - \int_{\infty}^M \vec E . \mathrm d \vec M}\)
La circulation ne dépendant pas du chemin suivi, quel est le chemin le plus simple pour aller de \(\infty\) à \(M\) ?
Solution simple
\(V = \frac{\lambda}{2 \epsilon_0} \frac{R}{\sqrt{R^2 + z^2}}\)
Solution détaillée
La circulation de \(\vec E\) ne dépendant pas du chemin suivi le chemin le plus simple pour aller de l'\(\infty\) à \(M\) est un parcours le long de l'axe \(Oz\). Dans ce cas, \(\mathrm d \vec M = \mathrm d z ~ \vec u_z\).
\(\displaystyle{V(M) = - \int_{\infty}^M \frac{\lambda R}{2 \epsilon_0} \frac{z}{\Big( R^2 + z^2 \Big)^{\frac 3 2}} \vec u_z ~ \mathrm d z ~ \vec u_z}\)
\(\displaystyle{V(M) = - \int_{\infty}^{z_M} \frac{\lambda R}{2 \epsilon_0} \frac{z}{\Big( R^2 + z^2 \Big)^{\frac 3 2}} \mathrm d z}~\)car \(~\vec u_z . \vec u_z = 1\)
\(\displaystyle{V(M) = - \frac{\lambda R}{2 \epsilon_0} \int_{\infty}^{z_M} \frac{z}{\Big( R^2 + z^2 \Big)^{\frac 3 2}} \mathrm d z}\)
Posons \(R^2 + z^2 = u\) et \(2 ~ z ~ \mathrm d z = \mathrm d u\)
\(\displaystyle{\int \frac{z} {\Big( R^2 + z^2 \Big)^{\frac 3 2}} \mathrm d z = \int \frac{ u^{ - \frac{3}{2} } }{2} \mathrm d u = \frac{1}{2} \left[ \begin{array}{lc} \frac{u^ { - \frac{1}{2} } }{ - \frac{1}{2}}\end{array} \right] = - u ^{ - \frac{1}{2} } }\)
\(V(M) = \frac{\lambda R}{2 \epsilon_0} \left[ \frac{1}{\sqrt{ R^2 + z^2 }} \right]_{\infty}^{z_M} = \frac{\lambda R}{2 \epsilon_0} \frac{1}{ \sqrt{R^2 + z_M^2} }\)
\(V = \frac{\lambda R}{2 \epsilon_0 \sqrt{R^2 + z^2}}\)
Ce résultat peut être trouvé également par calcul direct .