Potentiel V créé par une distribution discrète : calcul direct du potentiel 1/1
Partie
Question
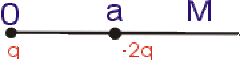
Sur un axe \(Ox\) , on place une charge positive \(q\) en \(O\) et une charge négative \(-2q\) au point d'abscisse \(a\).
a) Quelle origine des potentiels est-il logique de prendre ?
b) Le potentiel peut-il s'annuler en un point \(M\) d'abcisse \(O < x < a\) ?
c) Le potentiel peut-il s'annuler en un point \(M\) d'abcisse \(x < O\) ?
d) Le potentiel peut-il s'annuler en un point \(M\) d'abcisse \(x > a\) ?
Aide simple
a) _____________
b)
\(\displaystyle{V_i = \sum \frac{Q_i}{4 \pi \epsilon_0 ~ r_i}}\)
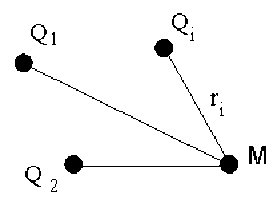
c) idem b)
d)__________________
Aide détaillée
a) Dans la formule \(\displaystyle{V_i = \sum \frac{Q_i}{4 \pi \epsilon_0 ~ r_i}}\), \(r_i\) est une distance qui doit être positive .
Rappel de cours
Voir la page V créé par une source quelconque
Solution simple
a) ___________
b) \(x = \frac{a}{3}\)
c) \(x = - a\)
d) ___________
Solution détaillée
a) Il est logique de poser que loin des charges, il n'y a plus d'influence des sources et que à l'infini \(V = 0\) : origine des potentiels \(V(\infty) = 0\).
b)
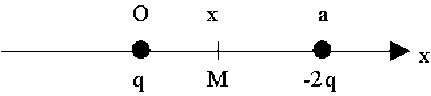
\(V = \frac{q}{4 \pi \epsilon_0 ~ x} + \frac{- 2 q}{4 \pi \epsilon_0 ~ (a - x)}\)
\(V = 0\) pour \(\frac{1}{x} = \frac{2}{(a - x)}\)
\(x = \frac{a}{3}\)
Pour que les deux potentiels se compensent, la distance entre \(M\) et \(- 2q\) doit être le double de celle entre \(M\) et \(q\) puisque le potentiel varie en inverse de la distance .
c)
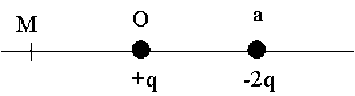
\(V = \frac{q}{4 \pi \epsilon_0 ~ |OM|} + \frac{- 2 q}{4 \pi \epsilon_0 ~ (a + |OM|)} = \frac{q}{4 \pi \epsilon_0 ~ (-x)} + \frac{- 2 q}{4 \pi \epsilon_0 ~ (a + -x)}\)
En effet la distance \(|OM| = - x\) car \(x < 0\).
\(V = 0\) pour \(- \frac{1}{x} = \frac{2}{a - x}\)
\(x = - a\)
Pour que les deux potentiels se compensent, la distance entre \(M\) et \(- 2q\) doit être le double de celle entre \(M\) et \(q\) puisque le potentiel varie en inverse de la distance.
d) Le point \(M\) étant plus près de la charge la plus forte, le potentiel créé par \(q\) (charge plus faible et plus éloignée) ne peut compenser celui qui est créé par \(2q\) .