Ion dans un champ magnétique (Q1)
Durée : 8 mn
Note maximale : 8
Question
Un point matériel portant une charge \(q ( > 0)\) est soumis à l'action d'un champ magnétique uniforme \(\vec{B}\): la force qui agit sur lui est égale à \(q\vec{v}\wedge\vec{B}\)
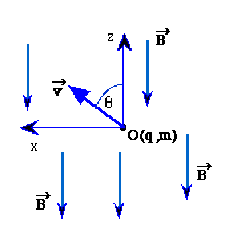
Par rapport au repère \(Oxyz\) , lié à un référentiel galiléen, où \(\vec{B}=B\vec{u_z}\) avec \(B<0\). écrivez l'équation vectorielle du mouvement de ce point matériel de masse \(m\).
Sachant qu'à l'instant \(t = 0\), le point matériel se trouve au point \(O\) et que sa vitesse est
\(\vec{v}(0)=v\sin\theta\vec{u_x}+v\cos\theta\vec{u_z}\) où \(v>0\).
déterminez la nature de l'hodographe dans l'espace des vitesses à trois dimensions.
Décrire le mouvement du vecteur vitesse dans cet espace.
Solution
L'Equation Fondamentale de la Dynamique s'écrit :
\(q\vec{v}\wedge\vec{B}=\frac{m\vec{dv}}{dt}\)
(1 point)
En projetant sur l'axe \(Oz\) du repère, on obtient , \(0=\frac{dv_z}{dt}\) car \(\vec{v}\wedge\vec{B}\perp u_z\): donc \(v_z\) est conservé.
(2 points)
En multipliant l'Equation Fondamentale par \(\vec{v}\), on obtient
\(0=m\vec{v}.\left(\frac{d\vec{v}}{dt}\right)=\left(\frac{m}{2}\right)\frac{d\vec{v}^2}{dt}\) car \(\vec{v}\wedge\vec{B}\perp{v}\)
donc \(v=|\vec{v}|\) est conservé.
(2 points)
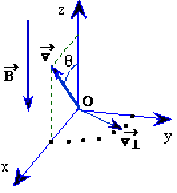
Ainsi, dans l'espace des vitesse à trois dimensions, l'hodographe est un cercle de rayon \(v \sin\theta\) situé dans un plan perpendiculaire à l'axe \(Oz\) et centré au point \((0,0,v\cos\theta)\).
(1 point)
On peut écrire l'Equation Fondamentale sous la forme :
\(\frac{d\vec{v}}{dt}=\left(-q\frac{\vec{B}}{m}\right)\wedge\vec{v}=\vec{\Omega}\wedge\vec{v}\)
(1 point)
Cela montre que l'extrémité du vecteur \(\vec{v}\) parcourt le cercle avec la pulsation \(\Omega\), dans le sens direct car \(\Omega > 0\).
(1 point)