Réfraction d'une particule.
Durée : 10 mn
Note maximale : 10
Question
Par rapport à une direction donnée \((x'x)\), l'espace est divisé en deux régions : dans l'une \((x > 0)\), un point matériel de masse \(m\) a une énergie potentielle \(U_+\), dans l'autre \((x < 0)\), l'énergie potentielle est égale à \(U_- > U_+\).
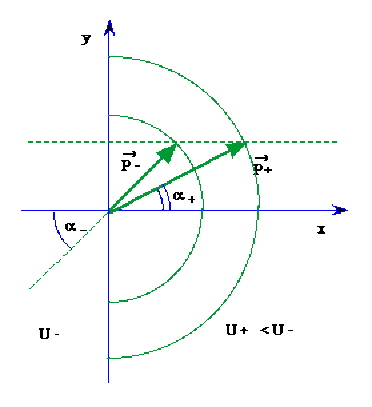
Initialement, le point matériel se trouve en un point où \(x < 0\) et sa quantité de mouvement est égale à \(\vec{p}\): il rencontre le plan \(x=0\) au point \(O\) et pénètre dans la région où \(x>0\).
Calculez l'impulsion communiquée au point matériel lorsqu'il traverse le plan.
Montrez que sa trajectoire est déviée au passage du plan.
Trouvez la relation qui lie les angles \(\alpha_-\) et \(\alpha_+\) qui caractérisent les directions de \(\vec{p}_-\) et \(\vec{p}_+\) par rapport à \(Ox\).
Montrez qu'un choix judicieux de l'origine des énergies permet de donner à cette relation la forme de la loi de Descartes en optique : quelle grandeur tient lieu d'indice de réfraction ?
Solution
L'énergie potentielle étant uniforme de part et d'autre du plan \(x = 0\),
(1 point)
le point matériel est libre dans chaque région \((x > 0)\) et \((x < 0)\) : ainsi, les trajectoires sont des demi-droites.
(1 point)
En traversant ce plan, le point matériel est soumis à une impulsion due au gradient de \(U\), \(U_+-U_-\), dirigé suivant \(Ox\),
\(\displaystyle{\int\vec{f}dt=\Delta p\vec{u_x}}\)
(2 points)
ainsi la composante \(p_y\) de \(\vec{p}\) parallèle au plan est conservée.
(1 points)
La conservation de l'énergie mécanique du point matériel permet de connaître la variation de \(p^2\):
\(\displaystyle{\frac{{p_-}^2}{2m}+U_-=\frac{{p_+}^2}{2m}+U_+}\)
(1 point)
De l'expression de \(\displaystyle{\sin\alpha=\frac{p_y}{p}}\), on tire :
\(\frac{sin\alpha_+}{\sin\alpha_-}=\left(\frac{p+y}{p-y}\right)\left(\frac{p_-}{p_+}\right)=\frac{p_-}{p_+}=\left(\frac{1+2m(U_+-U_-)}{{p_+}^2}\right)^{1/2}\)
(2 points)
L'énergie potentielle étant déterminée à une constante près, on peut la fixer de sorte que
\(E = 0\) et donc \(T + U = 0\) avec \(\displaystyle{T=\frac{p^2}{2m}}\) et \(U<0\) .
On a alors \(\frac{p_-}{p_+}=\left(\frac{1-(U_+-U_-)}{U_+}\right)^{1/2}=\sqrt{\frac{U_-}{U_+}}\)
(1 point)
et finalement, \(\sqrt{-U_+}\sin\alpha_+=\sqrt{-U_-}\sin\alpha_-\)
On voit que la grandeur \(\sqrt{-U}\) joue le rôle d'un indice de réfraction.
(1 point)