Pendule
Durée : 9 mn
Note maximale : 9
Question
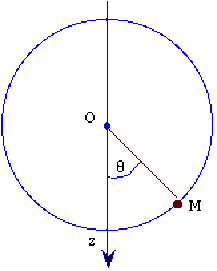
Un objet de petite taille de masse m qu'on peut assimiler à un point matériel est relié par une tige rigide de longueur \(l\) et de masse négligeable à un point fixe \(O\).
Il est abandonné sans vitesse initiale à une altitude inférieure à celle de \(O\).
Montrez que l'équation horaire du mouvement du point matériel sur un cercle situé dans un plan vertical peut être obtenue à partir de la relation exprimant la conservation de l'énergie mécanique.
Montrez qu'on retrouve aussi l'équation angulaire du mouvement (projection orthoradiale de l'Equation Fondamentale de la Dynamique) à partir de cette relation.
Solution
Le point matériel est soumis à l'action de la pesanteur et à la tension du fil perpendiculaire au déplacement.
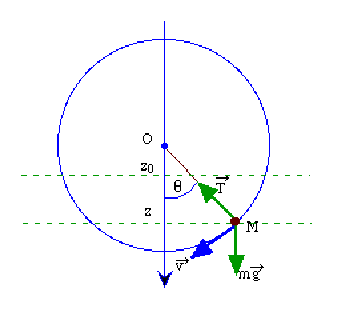
(2 points)
Ainsi, la tension ne travaille pas et on peut écrire \(\displaystyle{W_g=\frac{mv^2}{2}=mg(z-z_0)}\) car le poids dérive du potentiel \(-mgz + U_0\).
Cette relation exprime la conservation de l'énergie mécanique \(\displaystyle{E=\frac{mv^2}{2}-mgz+U_0}\)
(2 points)
Si on repère la position du point matériel sur le cercle par l'angle \(\theta\) tel que
\(z=l(1-\cos\theta)\) , on a \(v_2=2gl(\cos\theta-\cos\theta_0)\)
(1 point)
Donc, \(v=l\dot{\theta}=\sqrt{2gl(\cos\theta-\cos\theta_0)}\)
et pour de petits angles \(\displaystyle{\dot{\theta}=\sqrt{\left(\frac{g}{l}\right)({\theta_0}^2-\theta^2)}}\)
(2 points)
On obtient \(\displaystyle{\frac{d\theta}{\sqrt{{\theta_0}^2-\theta^2}}=\sqrt{\frac{g}{l}}dt}\) dont la solution est \(\displaystyle{\theta=\theta_0\cos\left(\sqrt{\frac{g}{l}}t\right)}\)
(1 point)
En dérivant par rapport au temps, on obtient \(2v\dot{v}=2gl(-\sin\theta)\dot{\theta}\)
soit, avec \(v=l\dot{\theta}\), l'équation \(\ddot{\theta}=\left(-\frac{g}{l}\right)\theta\) pour de petits angles.
(1 point)