Introduction

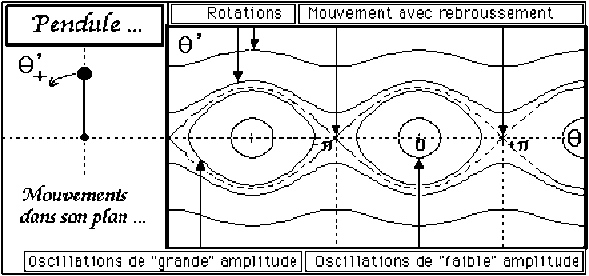
L'étude du pendule simple dans le plan de phase \((\theta,\theta')\) permet de fournir des solutions y compris dans le cas (non-linéaire) des mouvements d'amplitude quelconque (schéma ci-dessous).

La vitesse tangentielle est \(V_t = R.\theta' \phi\) , l'énergie cinétique est : \(E_c = m . R^2 \frac{\theta'^2}{2}\)

Prenant la position d'équilibre \((\theta = 0)\) pour origine des potentiels, l'énergie potentielle est alors :

\(E_p = m.g.R.(1 - \cos \theta)\)

Le système étant supposé isolé (pas de frottement), son énergie totale reste constante (notée \(K\)), soit :

\(E_p + E_c = K = m.g.R.(1 - \cos \theta) + \Big( \frac{m . R^2}{2} \Big) . \theta'^2\)

d'où : \(\frac{R}{2 g} \theta'^2 = \frac{K}{m g R} - 1 + \cos \theta\)

Cette relation décrit l'ensemble des trajectoires à énergie constante.

Ces différentes trajectoires sont représentées (ci-dessus) dans l'espace des phases \((\theta,\theta')\).

Si l'énergie totale du pendule est supérieure à \(2mgR\), il effectuera des rotations toujours dans le même sens.

Dans le cas particulier où l'énergie totale du système est \(K = 2mgR\), la trajectoire dans l'espace des phases possède un point de rebroussement en \(\theta = \pi\), ce qui correspond à un point d'arrêt du mouvement dans l'espace physique en (\(\theta = \pi\)) avec changement possible du signe de la vitesse \(R.\theta'\).

Si l'énergie totale du pendule est inférieure à \(2mgR\), il effectuera des oscillations d'amplitude plus ou moins grande (selon la valeur de son énergie).