Modèle et représentation.
Grosso-modo, on peut définir la démarche globale de représentation par la mise en relation d'un ensemble d'éléments de la réalité par laquelle ces éléments prennent du sens. Cette définition (très ouverte) s'applique aussi bien au processus de construction lui-même qu'au résultat logique de cette construction.
Ce processus ne met pas en oeuvre une logique entièrement consciente et n'est pas complètement explicable : on s'autorisera ici à ne considérer que sa rationalité interne, i.e. les relations entre différents champs (réalité, modèle, théorie) que met en évidence et que construit ce processus de représentation.
Il faut préciser ce que l'on entend par la réalité : ce n'est pas un "donné" expérimental, car la réalité passe par le filtre des représentations pré-existantes et a besoin d'un support ou d'un langage minimum (théorie) pour être reconnue comme telle. Ce niveau préalable de représentations permet ainsi d'exprimer une part de réalité, mais ce faisant (comme tout langage) la limite à l'intérieur d'un cadre conceptuel pré-défini. Ce filtre est ainsi un premier niveau de réduction de la réalité par lequel le "fait réel" devient "fait perçu" pour devenir ensuite "fait scientifique".
Le fait perçu est donc modélisé (un "point matériel" n'est qu'un concept à l'intérieur d'un modèle déterminé), puis paramétré en relation avec un espace de représentation théorique (paramètrage sur les Réels, par exemple, permettant de représenter le concept de masse ou de position).
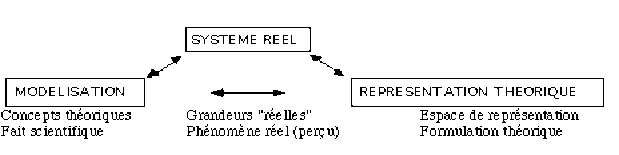
Dans le cas par exemple où l'on repérera la reproduction "plus ou moins" régulière d'un phénomène, on pourra le modéliser par le concept de périodicité, modélisation qui a son tour induira de le représenter dans un espace vectoriel de fonctions périodiques, représentation qui en retour posera des exigences théoriques spécifiques au niveau du modèle. On traitera ultérieurement en détail cet exemple déjà cité.
Dans le cas (qui sera traité auparavant) où l'on s'intéresse à un système réel constitué par \(N\) masses reliées entre elles par des ressorts, on va chercher à décrire l'état du système par une grandeur (que l'on notera \(\Psi\)) qui puisse caractériser l'ensemble des positions de chacune des \(N\) masses.
"Naturellement" (parce que l'idée d'Espace Vectoriel est préexistante) on modélisera l'état du système par un Vecteur Etat \(\Psi\), représenté dans \(R^N\) par un N-uplet dont chacun des éléments représente l'état (c'est-à-dire par exemple la position sur un axe) de chacune des \(N\) masses constituant le système (si chacune des masses est assujettie à ne se déplacer que dans une seule direction).
Alors, pour pouvoir utiliser les propriétés de l'algèbre linéaire (opérateurs matriciels sur \(R^N\)), on peut être tenté de réduire la réalité au cas modélisé par des actions (dues aux ressorts) qui seraient représentées par des forces variant linéairement avec leur allongement.
On peut aussi se placer dans le cas d'un modèle plus simple encore qui présupposerait, de plus, qu'aucune force ne vient freiner les mouvements.
Le mode de représentation théorique permet alors d'envisager de modéliser l'évolution de l'état du système au cours du temps, chacune des "masses ponctuelles" devant satisfaire au principe fondamental de la dynamique.
Dès lors, l'espace de représentation \(R^N\) (N-uplets de paramètres réels) ne convient plus, puisqu'il ne s'agit plus uniquement de représenter la valeur de l'état du système (la représentation qu'en donnerait sa photo) à un instant donné, mais de rendre compte de son évolution : il convient alors de construire un autre espace de dimension \(N\), dont chaque N-uplet est un ensemble de \(N\) fonctions du temps, telles que chacune d'elles puisse représenter l'évolution de chacune des \(N\) masses. C'est la possibilité théorique de construire un tel espace vectoriel qui valide le processus.
Bien que très schématique, cet exemple montre la circularité de la démarche qui peut conduire à l'élaboration des représentations.
Dans ces conditions, on notera \(\Psi(t)\) l'état du système, et \(\ddot \Psi(t)\) sera son accélération.
Compte tenu de la modélisation linéaire et du non amortissement (pas de dissipation d'énergie), l'évolution du système devra satisfaire une équation d'évolution représentée par un opérateur matriciel \(U\) dont les éléments caractérisent le système physique modélisé (par exemple les masses d'un système masses-ressorts).
Cette équation sera du type : \(\ddot \Psi(t) = U ~ . ~ \Psi(t)\)
soit : \(~~ \left| \begin{array}{c} \ddot \Psi^1 \\ \ddot \Psi^2 \\ ... \\ ... \\ \ddot \Psi^N \end{array} \right| = \left| \begin{array}{ccccc} a & b & ... & ... & ... \\ c & d & ... & ... & ... \\ ... & ... & ... & ... & ... \\ ... & ... & ... & ... & ... \\ ... & ... & ... & ... & ... \end{array} \right| ~ . ~ \left| \begin{array}{c} \Psi^1 \\ \Psi^2 \\ ... \\ ... \\ \Psi^N \end{array} \right|\)
Dans toute la suite de ce cours, on représentera les vibrations d'un système selon ce formalisme, dans lequel les composantes d'un état sont désignées par un exposant (numéro de la ligne).
Dans cet espace de représentation, un état particulier est un vecteur que l'on devra spécifier par un indice (placé en bas).