Propagation de champs vectoriels
Partie
Question
- A -
Une onde monochromatique représentée par \(\vec V_1\) se propage par ondes planes dans un milieu homogène, isotrope avec la vitesse \(v\).
Dessiner (figure 1) le champ \(\vec V_1 (r, t)\) le long des droites \((D)\) et \((D')\).
Préciser la direction de propagation, celle des plans d'onde ainsi que la direction de polarisation.
Ecrire la forme analytique de cette onde sous la forme \(\vec V_1 (x,y,z,t)\) [en fonction des données : \(\lambda_1\) et \(v\)].
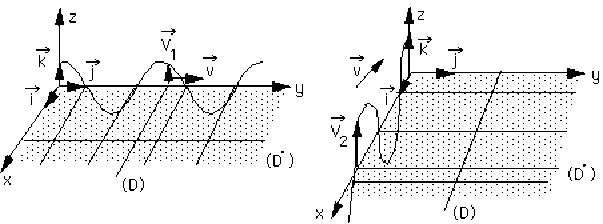
Les figures 1 et 2 représentent les champs \(\vec V_1\) et \(\vec V_2\) et leur longueur d'onde (à un instant \(t\)).
- B -
Une onde monochromatique représentée par \(\vec V_2(r, t)\) se propage par ondes planes dans un milieu homogène, isotrope avec la vitesse \(v\).
Dessiner (figure 2) le champ \(\vec V_2 (r, t)\) le long des droites \((D)\) et \((D')\).
Préciser la direction de propagation, celle des plans d'onde ainsi que la direction de polarisation.
Écrire la forme analytique de cette onde sous la forme \(\vec V_2 (x,y,z,t)\) [en fonction des données : \(\lambda_2\) et \(v\)].
- C -
On considère les champs électriques se propageant à la vitesse \(v\) :
\(\vec E_1 (x,y,z,t) = \cos (\omega t - Ky) . \vec k ~~\) et \(~~ \vec E_2 (x,y,z,t) = \cos (\omega t + Kx) . \vec k\)
Expliciter les vecteurs d'onde \(\vec K_1\) et \(\vec K_2\) (norme et direction).
Exprimer le champ résultant \(\vec E = \vec E_1 + \vec E_2\).
Montrer qu'il se propage.
Déterminer son vecteur d'onde \(\vec K'\) (norme et direction).
Cette onde se propage-t-elle par ondes planes ?
Déterminer le champ \(\vec B\) associé au champ électrique \(\vec E = \vec E_1 + \vec E_2\) .
Pourquoi ne peut-on utiliser directement la relation vectorielle : \(\vec B = \Big( \frac{1}{v} \Big) \vec u \wedge \vec E\) entre les champs de vecteurs \(\vec E\) et \(\vec B\) ?
Comment aurait-on pu calculer directement \(\vec B\) à partir de \(\vec E\) ?
Aide simple
Représentation du problème : consultez les animations suivantes.
Montre la propagation de deux systèmes de vagues croisées.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Montre la propagation résultant de la somme des deux systèmes de vagues.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
La vue de dessus montre que le système de vagues résultant se propage, selon une direction bissectrice des directions de propagation composantes.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Techniquement :
Questions A et B : Revoyez les définitions (direction de propagation, onde progressive, onde régressive, direction de polarisation).
Question C : Revoyez l'expression de la propagation en faisant intervenir le vecteur d'onde : il s'agit de montrer que la somme des ondes (se propageant respectivement selon \(OX\) et \(OY\)) a la forme d'une onde qui se propage (ici : selon la bissectrice de \(OX\) et de \(OY\)).
Solution détaillée
- A -
- A.1 -
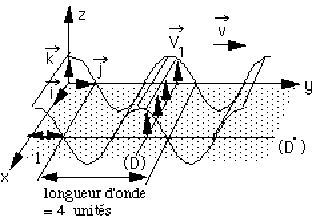
- A.2 -
Propagation selon le vecteur unitaire : \(\vec j\)
Plans d'onde parallèles au plan \((x, z)\)
Polarisation dans la direction du vecteur unitaire : \(\vec k\)
- A.3 -
La forme générale de la propagation, dans la direction et le sens de \(y\), d'une onde sinusoïdale scalaire est :
\(V_1 (x, y, z, t) = 1 . \cos (K_1 . y - \omega_1 . t + \varphi_1) \equiv \cos \big( K_1 (y - v_1 . t - y_0) \big)\)
On dit que cette onde est progressive, ce qui signifie qu'elle "progresse" (se propage) dans le sens de référence \(y\). Dans le cas contraire (où l'onde se propage dans le sens opposé au sens de référence), on dit que cette onde est régressive. Dans cette expression : \(\varphi_1\) (ou \(y_0\)) représente le déphasage en \(t=0\).
\(v_1\) = vitesse de l'onde \(V_1\) dans la direction \(Oy \equiv v\) .
\(\lambda_1\) = longueur d'onde (période spatiale) = \(4\) (d'après le schéma).
\(K_1 = \frac{2 \pi}{\lambda_1} ~~~~ \Rightarrow ~~ K_1 = \frac{\pi}{2}\)
\(v_1 = \frac{\omega_1}{K_1} ~~~~ \Rightarrow ~~ \omega_1 = v_1 . K_1 = v . \frac{\pi}{2}\)
\(\vec V_1 (x, y, z, t) = \vec k . \cos \left [ \frac{\pi}{2} (y - v.t - y_0) \right]\) représente la propagation, dans la direction et le sens de \(y\), d'une onde sinusoïdale polarisée selon le vecteur \(\vec k\).
Pour déterminer \(y_0\) ou le déphasage \(\varphi_1\), on utilise la valeur de l'onde en \(t=0\).
Dans cette expression, la valeur \(y_0 = 0\) (ou \(\varphi_1= 0\)) satisfait la condition initiale représentée sur le schéma :
\(y = 0 ~ \mathrm{ et } ~ t=0 ~~~~ \Rightarrow ~~ \vec V_1 = \vec k . \cos \left[ \frac{\pi}{2} (-y_0) \right]\) , et \(~~ \vec V_1 = \vec k ~~~~ \Rightarrow ~~ y_0 = 0\)
- B -
- B.1 -
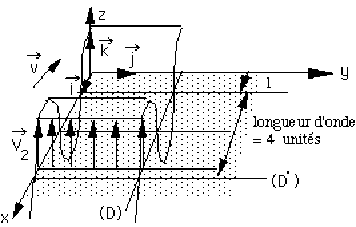
- B.2 -
Propagation selon le vecteur : \(- \vec i\)
Plans d'onde parallèles au plan \((y, z)\)
Polarisation dans la direction du vecteur unitaire : \(\vec k\)
- B.3 -
De la même façon que précédemment, la forme générale de la propagation, dans la direction et le sens de \(x\), d'une onde sinusoïdale polarisée selon le vecteur \(\vec k\) s'exprime :
\(\vec V_2 (x, y, z, t) = \vec k . \cos \big[ K_2 (x - v_2 . t - x_0) \big]= \vec k . \cos \big[K_2.\big( (x - x_0) - v_2 . t \big) \big]\)
Dans cette expression : \((x - x_0) = X\) représente la position par rapport à la condition initiale \(x_0\). On détermine comme précédemment la valeur de \(x_0\) en fonction des données du problème.
Ici : en \(x=0\) et \(t=0\), l'onde a son amplitude maximale : \(\vec V_2 = \vec k\), d'où \(x_0 = 0\).
Comme précédemment (sur le schéma) : \(\lambda_2 = 4 ~~~~ \Rightarrow ~~ K_2 = \frac{\pi}{2} = K_1\)
En résumé, dans ce problème :
\(\vec V_1 = \vec k . \cos \left[ \frac{\pi}{2} (y - v.t) \right]\) (onde progressive)
\(\vec V_2 = \vec k . \cos \left[ \frac{\pi}{2} (x + v.t) \right]\) (onde régressive)
- C -
On considère les champs : \(\vec E_1 = \vec k . \cos (\omega . t - K_1 . y)~\) et \(~ \vec E_2 = \vec k . \cos (\omega . t + K_2 . x)\)
- C.1 -
Un vecteur d'onde \(\vec K\) a pour norme \(K = \frac{2 \pi}{\lambda}\) et pour direction et sens ceux définis par la propagation. Les ondes précédentes s'expriment donc, en fonction des vecteurs d'onde :
\(\vec E_1 = \vec k . \cos (\omega . t - \vec K _1 . \vec r)~\) et \(~\vec E_2 = \vec k . \cos (\omega . t - \vec K _2 . \vec r)\)
Les signes " - " signifient que les ondes sont toujours "progressives" si on prend comme sens de référence celui de la propagation (car le sens de la propagation est justement défini par le vecteur d'onde).
\(\begin{array}{llcl} \mathrm{Soit : } & - K_1 . y = - \vec K_1 . \vec r & \mathrm{ } \mathrm{ } \mathrm{ avec } & \mathrm{ } \vec K_1 = \frac{2 \pi}{\lambda_1} \vec j \\ \mathrm{et : } & + K_2 . x = - \vec K_2 . \vec r & \mathrm{ } \mathrm{ } \mathrm{ avec } & \mathrm{ } \vec K_2 = \frac{2 \pi}{\lambda_2} (- \vec i) \end{array}\)
Noter que, comme \(\lambda_1 = \lambda_2\) , on a donc : \(K_1 = K_2\)
- C.2 -
Champ résultant : \(~ \vec E = \vec E_1 + \vec E_2 = \vec k . \big[ \cos (\omega . t - \vec K_1 . \vec r ) + \cos (\omega . t - \vec K_2 . \vec r ) \big]\)
Sachant que : \(~ \cos p + \cos q = 2 ~ . ~ \cos \frac{p + q}{2} ~ . ~ \cos \frac{p - q}{2}\)
\(\Rightarrow ~~ \vec E = 2 \vec k ~ . ~ \cos \left[ \omega . t - \left( \frac{\vec K_1 + \vec K_2}{2} \right) . \vec r \right] ~ . ~ \cos \left[ \left( \frac{\vec K_1 - \vec K_2}{2} \right) . \vec r \right]\)
\(\frac{\vec K_1 + \vec K_2}{2} = \frac{\pi}{\lambda} (\vec j - \vec i) = \vec K ~~~~~~~~ \frac{\vec K_1 - \vec K_2}{2} = \frac{\pi}{\lambda} (\vec i + \vec j)\)
\(\vec E = 2 \vec k ~ . ~ \cos \left[ \frac{\pi}{\lambda} (\vec i + \vec j) . \vec r \right] ~ . ~ \cos \left[ \omega . t - \vec K' . \vec r \right]\)
avec \(~~ \vec K' = \frac{\pi}{\lambda} (\vec j - \vec i) ~~~~ \Rightarrow ~~ \textrm{propagation dans la direction et le sens de } \vec K'\).
\(\vec j - \vec i = \sqrt{2} ~~\),\(\quad\) \(~~ \vec K' = \frac{\pi \sqrt{2}}{\lambda} \vec u ~~\) avec \(~ \vec u = \frac{\vec j - \vec i }{\Big|\Big| \vec j - \vec i \Big|\Big|}\)
Cette onde n'est pas plane car dans le plan \(\perp\) \(\vec u\), \(\vec E\) dépend de \(\vec r\) par le facteur : \(\cos \Big( \frac{\pi}{\lambda} (\vec i + \vec j) . \vec r \Big)\) .
La période spatiale de la propagation est : \(\begin{array}{l} \Lambda' = \frac{2 \pi}{K'} = \frac{2 \pi \lambda}{\pi \sqrt{2}} \\ \Lambda' = \sqrt{2} . \lambda \end{array}\)
L'amplitude des maximums est obtenue pour tous les points où : \(\cos \Big( \frac{\pi}{\lambda} (\vec i + \vec j) . \vec r \Big) = 1\) .
C'est donc l'amplitude maximum de chacune des composantes multipliée par 2.
- C.3 -
Le champ total \(\vec E\) ne se propage pas par onde plane \(~ \Rightarrow ~\) On n'a pas le droit de déterminer \(\vec B\) par la relation \(\frac{1}{v} \vec u \wedge \vec E\), mais séparément oui, car chacune des composantes de \(\vec E_{\mathrm{Total}}\) est plane.
\(\begin{array} {l} \vec B_1 = \frac{1}{v} \vec j \wedge \vec E_1 = \frac{1}{v} \vec i \cos (\omega . t - K_1 . y) \\ \\ \vec B_2 = \frac{1}{v} (- \vec i) \wedge \vec E_2 = \frac{1}{v} \vec j \cos (\omega . t - K_2 . x) \end{array} ~~~~~~~~ \vec B_{\mathrm{Total}} = \vec B_1 + \vec B_2\)
Dans le cas où l'on connait un champ \(\vec E\) qui ne se propage pas par onde plane, on peut également utiliser les équations de Maxwell car, dans tous les cas : \(\vec E_{\mathrm{Total}}\) et \(\vec B_{\mathrm{Total}}\) satisfont Maxwell.
\(\vec E_{\mathrm{Total}} ~~~ \Rightarrow ~~ \overrightarrow{\mathrm{rot}} ~ \vec E_T = \frac{\partial \vec B_T}{\partial t}\) , ce qui permet éventuellement d'obtenir \(\vec B_T\) par intégration.
Montre la propagation de deux systèmes de vagues croisées.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Montre la propagation résultant de la somme des deux systèmes de vagues.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
La vue de dessus montre que le système de vagues résultant se propage, selon une direction bissectrice des directions de propagation composantes.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.