Réflexion métallique en incidence normale
Partie
Question
- A -
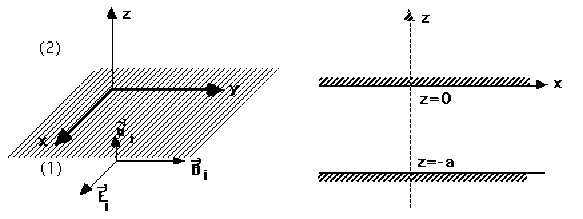
Soit \((xOy)\) le dioptre plan séparant deux milieux notés respectivement \((1)\) et \((2)\). Le milieu \((1)\) défini par \(z < 0\) est transparent. Le milieu \((2)\) défini par \(z > 0\) est métallique. Ce dioptre de séparation est supposé parfaitement réfléchissant.
Comment peut se traduire cette propriété physique ? Dans toute la suite, on se limite au cas de l'incidence normale d'une onde monochromatique, plane, polarisée rectilignement. On prendra par exemple \(\vec E_i\) polarisé suivant \(Ox\).
De quelle variable d'espace dépend \(\vec E_i\) ? Justifier l'expression du champ électrique : \(\vec E_i = E_{io}. \vec i . \cos (\omega . t - K . z)\) , avec \(\vec K_i = \vec u_i . K\)
Evaluer \(\vec u_r\) pour l'onde réfléchie. En appelant \(\psi_r\) le déphasage de l'onde réfléchie par rapport à l'onde incidente, écrire les expressions complètes de \(\vec E_r\) , \(\vec B_i\) et \(\vec B_r\) .
Ecrire dans le plan de réflexion (\(z = 0\)) la conservation de la composante tangentielle du champ électrique. En déduire \(\psi_r\) , ainsi que \(E_{ro}\) puis \(B_{ro}\) .
Ecrire finalement les expressions complètes des champs :
\(\vec E(z,t) = \vec E_i (z, t) + \vec E_r (z, t) ~~~~ [ \forall z < 0 ]\)
\(\vec B(z, t) = \vec B_i (z, t) + \vec B_r (z, t)\)
Montrer que dans le milieu \((1)\) \(\vec E\) et \(\vec B\) peuvent s'écrire :
\(\vec E (z, t) = 2 . E_{io}. \vec i . \sin (\omega . t) . \sin (K.z)\)
\(\vec B (z, t) = \frac{2}{V} . E_{io}. \vec j . \cos (\omega . t) . \cos (K.z)\)
Quelle est la nature du phénomène physique représenté par cette expression ? A quel autre type de système physique ce phénomène peut-il vous faire penser ?
Indiquer les côtes \(z_0\) des plans caractérisés par des noeuds :
- du champ électrique : \(\vec E (z_0, t) = 0 ~~~~ \forall t\)
- du champ magnétique : \(\vec B (z_0, t) = 0 ~~~~ \forall t\)
Représenter sur deux schémas distincts l'évolution de \(\vec E\) et de \(\vec B\) le long de \(Oz\) à un instant \(t\) donné.
- B -
L'onde électromagnétique précédente (monochromatique, plane, polarisée rectilignement) arrive normalement à la surface parfaitement réfléchissante située en \(z = 0\).
On ajoute au dispositif précédent une autre surface métallique parfaitement réfléchissante, située en \(z = - a\) (figure 2).
Dessiner (figure 2) le champ \(\vec V_2 (r, t)\) le long des droites \((D)\) et \((D')\) .
Montrer que seules des ondes sinusoïdales de pulsation bien définie peuvent exister entre les deux miroirs. Déterminer ces pulsations.
A quel autre système physique (de type mécanique) ce dispositif est-il comparable ?
Aide simple
Représentation du problème : consultez les animations suivantes.
Superposition d'une onde progressive et d'une onde régressive de même amplitude (1)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
La réflexion totale (sur le plan métallique) du champ électromagnétique produit un champ électromagnétique réfléchi qui se propage en sens inverse, de même fréquence et de même amplitude.
La somme des deux champs électriques et la somme des deux champ magnétiques sont stationnaires.
Superposition d'une onde progressive et d'une onde régressive de même amplitude (2)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Les plans métalliques situés en \(z = 0\) et en \(z = L\) produisent des ondes réfléchies qui se superposent aux ondes incidentes.
Si la distance entre les plans métalliques est multiple de la demi-longueur d'onde, alors toutes les ondes progressives sont en phase, de même que toutes les ondes régressives sont en phase : leur somme est alors une onde stationnaire.
Techniquement :
Questions A et B : Revoyez les définitions (direction de propagation, onde progressive, onde régressive, direction de polarisation).
Question C : Revoir l'expression de la propagation en faisant intervenir le vecteur d'onde : il s'agit de montrer que la somme des ondes (se propageant respectivement selon \(OX\) et \(OY\)) a la forme d'une onde qui se propage (ici : selon la bissectrice de \(OX\) et de \(OY\)).
Rappel de cours
Voir la page Résultat général
Solution détaillée
- A -
- A.1 -
Réflexion métallique \(~~~ \Rightarrow ~~\) dans le milieu \((2)\), il n'y a pas d'onde transmise \(~~~ \Rightarrow ~~\) \(\vec E_2 = 0\)
Onde plane \(~~~ \Rightarrow ~~\) le trièdre \(\vec E_i\) , \(\vec B_i\) , \(\vec u_i\) est direct ; \(\vec u_i\) vecteur unitaire dans le sens de la propagation : \(\vec u_i = \vec k\)
\(\textrm{Plan d'onde} = (x, y)\) \(~~~ \Rightarrow ~~\) pas de dépendance en \(\left\{ \begin{array}{c} x \\ y \end{array} \right\}\) \(~~~ \Rightarrow ~~\) \(\left\{ \begin{array}{c} \vec E_i \\ \vec B_i \end{array} \right\}\) ne dépend que de \(z\).
- A.2 -
Monochromatique \(~~ \Leftrightarrow ~~\) une seule période spatiale \(\lambda\) avec \(\lambda = VT = \frac{V}{\nu}\)
Une seule fréquence \(u\) \(~~ \Leftrightarrow ~~\) un seul terme cosinus
\(\Rightarrow ~~ \vec E_i = \vec E_{io} . \vec i . \cos (c_0 . t - K_i . z)\) (progressive dans le sens \(z > 0\))
Milieu \((2)\) conducteur parfait \(~~~ \Rightarrow ~~\) \(\vec E_2 = 0 ~~ \Leftrightarrow ~~ \left\{ \begin{array}{c} E_{2t} = 0 \\ E_{2n} = 0 \end{array} \right\} ~~ \Rightarrow ~~ \left\{ \begin{array}{c} E_{1t} = 0 \\ D_{2n} = 0 \end{array} \right\}\)
D'où \(D_{1n} = 0 ~~~ \Rightarrow ~~ E_{1n} = 0\)
\(~~~ \Rightarrow ~~ \left\{ \begin{array}{c} E_{1t} = 0 \\ E_{1n} = 0 \end{array} \right\} ~~ \Leftrightarrow ~~ \vec E_1 = 0\)
Le plan de séparation \((z = 0)\) est un noeud du champ électrique dans la région \((1)\) comme dans la région \((2)\).
- A.3 -
Onde réfléchie :
D'après les lois de Descartes, on a nécessairement
\(\vec u_r = - \vec u_i ~~~ \Rightarrow ~~ \vec u_r = - \vec k\)
\(\Rightarrow ~~\) le plan d'onde de l'onde réfléchie est perpendiculaire à \(\vec k\) .
Tout plan \(z\) égal à une constante (en particulier le plan \((x, y)\)) est un plan d'onde.
\(\vec E_{1n} = 0 ~~ \Leftrightarrow ~~ \vec E_{in} + \vec E_{rn} = 0\)
D'après la polarisation de l'onde incidente : \(\vec E_{in} = 0 ~~~ \Rightarrow ~~ \vec E_{rn} = 0\)
\(\Rightarrow ~~\) les champs électriques incident et réfléchis sont tangentiels au plan du dioptre (\(z=0\)).
\(\vec E_i = E_{io} . \vec i . \cos (\omega . t - K_i . z)\) \(~~~ \Rightarrow ~~\) \(\vec E_r\) polarisé aussi selon \(\vec i\) pour que puisse être satisfaite la relation \(\vec E_i + \vec E_r = 0\) (en \(z=0\)).
La réflexion ne change pas la pulsation de l'onde (voir cours) \(~~~ \Rightarrow ~~\) l'onde réfléchie a la pulsation \(\omega\).
Forme de l'onde plane après réflexion : \(\vec E_r = E_{ro} . \vec i . \cos (\omega . t + K_r . z + \psi_r) ~\)
Puisque le champ électrique est nul dans le plan du dioptre (\(z=0\)), il en est de même pour le champ magnétique
\(\begin{array}{ll} \Rightarrow \vec B_1 = 0 \Leftrightarrow & \vec B_{in} + \vec B_{rn} = 0 \textrm{ et } \vec B_{it} + \vec B_{rt} = 0 \\ & \vec B_{in} = 0 \Rightarrow \vec B_{rn} = 0 ( \textrm{en } z = 0)\end{array}\)
\(\Rightarrow ~~\) Le champ magnétique réfléchi est polarisé tangentiellement au plan du dioptre.
\(\vec E_i\) étant une onde plane, on a donc :
\(\displaystyle{\vec B_i = \frac{1}{v} \vec u_i \wedge \vec E_i = \frac{1}{v} ( \vec k \wedge \vec i ) . E_{io} . \cos (\omega . t - K_i . z) = \frac{1}{v} . \vec j . E_{io} . \cos (\omega . t - K_i . z)}\)
\(\Rightarrow ~~\) L'onde \([\vec E_i , \vec B_i]\) est une onde plane.
En admettant que \(\vec E_r\) est aussi une onde plane (démonstration dans le cours), on a donc :
\(\begin{array}{lll} \vec B_r & = & \frac{1}{v} \vec u_r \wedge \vec E_r \\ & = & \frac{1}{v} (- \vec k) \wedge (- \vec i) . E_{ro} . \cos (\omega . t + K_r . z + \psi_r) \\ & = & \frac{1}{v} E_{ro} . \vec j . \cos (\omega . t + K_r . z + \psi_r) \end{array}\)
\(\Rightarrow ~~\) L'onde \([\vec E_r , \vec B_r]\) est une onde plane.
- A.4 -
\(z = 0 ~~~ \Rightarrow ~~ \vec E_i + \vec E_r = \vec 0 = \vec i . [E_{io} . \cos (\omega . t) + E_{ro} . \cos (\omega . t + \psi_r)]\)
Dans le plan \((z=0)\) : conservation de la composante tangentielle \(\forall t\) .
\(\Rightarrow ~~ [E_{io} . \cos (\omega . t) + E_{ro} . \cos (\omega . t + \psi_r)] = E_{io} . [ \cos (\omega . t) + \frac{E_{ro}}{E_{io}} . \cos (\omega . t + \psi_r)] = 0 ~~~~ \forall t\)
L'amplitude max. des cosinus étant égale à 1, cette relation ne peut être satisfaite \(\forall t\) que si le coefficient \(\frac{E_{ro}}{E_{io}}\) est lui-même égal à 1 en valeur absolue.
Si on considère les coefficients d'amplitudes [\(E_{io}\) et \(E_{ro}\)] comme positifs, alors :
\([\cos (\omega . t) + \cos (\omega . t + \psi_r)] = 0 ~~~~ \forall t\)
\(\Rightarrow ~~\) les termes \(\cos (\omega . t)\) et \(\cos (\omega . t + \psi_r)\) doivent être en opposition de phase : \(\psi_r = (2p+1) \pi\) (\(p\) entier).
\(\begin{array}{lll} \Rightarrow \mathrm{ } \vec E_r & = & E_{ro} . \vec i . \cos (\omega . t + K_r . z + \psi_r) \\ & = & - E_{io} . \vec i . \cos (\omega . t + K_r . z) \\ \mathrm{ }\vec B_r & = & \frac{1}{v} . E_{io} . \vec j . \cos (\omega . t + K_r . z + \psi_r) \\ & = & - \frac{1}{v} . E_{io} . \vec j . \cos (\omega . t + K_r . z) \\ & = & B_{ro} . \vec j . \cos( \omega . t + K_r . z) \end{array}\)
\(\Rightarrow ~~ B_{ro} = - \frac{1}{v} E_{io}\)
En résumé :
\(\begin{array}{llll} \vec E_i = E_{io} . \vec i . \cos (\omega . t - K_i . z) & & & \vec E_r = - E_{io} . \vec i . \cos (\omega . t + K_r . z) \\ \vec B_i = \frac{E_{io}}{v} . \vec j . \cos (\omega . t - K_i . z) & & & \vec B_r = - \frac{E_{io}}{v} . \vec j . \cos (\omega . t + K_r . z)\end{array}\)
- A.5 -
Les ondes incidente et réfléchie se propagent dans le même milieu, donc à la même vitesse. Elles ont donc même longueur d'onde \(~~\Rightarrow ~~ K_i = K_r = K\)
\(\vec E_1 (z,t) = \vec E_i (z,t) + \vec E_r (z,t) = E_{io} . \vec i . [\cos (\omega . t + K . z) - \cos (\omega . t + K . z)]\)
\(\vec B_1 (z,t) = \vec B_i (z,t) + \vec B_r (z,t) = \frac{E_{io}}{v} . \vec j . [\cos (\omega . t + K . z) + \cos (\omega . t + K . z)]\)
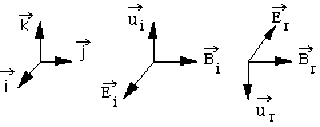
- A.6 -
En développant les expressions précédentes (en \(\cos (p+q)\) et \(\cos (p-q)\)), on trouve :
\(\vec E_1 (z, t) = 2 . E_{io} . \vec i . \sin (\omega . t) . \sin (K . z)\)
\(\vec B_1 (z, t) = 2 . \frac{E_{io}}{v} . \vec j . \cos (\omega . t) . \cos (K . z)\)
- A.7 -
L'expression ci-dessus de l'onde résultante dans la région \((1)\) représente une onde stationnaire :
\(\begin{array}{lclrl} \textrm{Noeuds de } \vec E_1 & & \sin (K.z) = 0 \Rightarrow K.z = m . \pi & \textrm{avec } K = \frac{2 \pi}{\lambda} & \Rightarrow z = \frac{\lambda}{2 \pi} m . \pi = m \frac{\lambda}{2} \\ \textrm{Noeuds de } \vec B_1 & & \cos(K.z) = 0 \Rightarrow K.z = n . \pi + \frac{\pi}{2} & & \Rightarrow z = \frac{\pi}{4} + n \frac{\lambda}{2} \end{array}\)
Superposition d'une onde progressive et d'une onde régressive de même amplitude (1)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
La réflexion totale (sur le plan métallique) du champ électromagnétique produit un champ électromagnétique réfléchi qui se propage en sens inverse, de même fréquence et de même amplitude.
La somme des deux champs électriques et la somme des deux champ magnétiques sont stationnaires.
- B -
- B.1 -
Dans la région entre les plaques se superposent une onde progressive et une onde régressive de même type que celles décrites dans l'exercice précédent.
- B.2 -
Ce qui change par rapport à l'exercice précédent est qu'il y a une condition de réflexion en \(z=0\) et une condition de réflexion en \(z = -a\).
\(z = 0 ~~~ \Rightarrow ~~ \textrm{noeud de } E\)
\(z = -a ~~~ \Rightarrow ~~ \textrm{noeud de } E\) impose \(- a = m \frac{\lambda}{2} ~~ \Leftrightarrow ~~ \lambda = \frac{- 2 a}{m}\) (\(m\) entier positif ou négatif).
Cette condition correspond à une pulsation \(\omega\) telle que : \(\lambda = \mathrm{c} T = \mathrm{c} \frac{2 \pi}{\omega}\)
\(\Rightarrow ~~ \omega = \frac{2 \pi \mathrm{c}}{\lambda}\)
\(\Rightarrow ~~\) la première valeur possible pour \(\lambda\) est : \(\lambda_1 = 2a\)
\(\Rightarrow ~~\) la première valeur possible pour \(\omega\) est : \(\omega_1 = \frac{2 \pi \mathrm{c}}{\lambda_1} = \frac{\pi \mathrm{c}}{a}\)
Les valeurs (positives) possibles pour \(\omega\) sont définies par :
\(\omega_n = n \frac{\pi \mathrm{c}}{a} = n . \omega_1\)
Cette condition sera retrouvée lors de l'étude des modes propres d'une corde fixée à ses extrémités. (Cette question n'aurait pas dû être posée ici...)
Remarque à propos des équations de Maxwell
Avec les valeurs précédentes, on peut calculer :
\(\overrightarrow{\mathrm{rot}} ~ \vec B = - \frac{\partial B_y}{\partial z} \vec i = - \vec i \frac{E_{io}}{\mathrm{c}} K . [\sin (\omega . t - K.z) - \sin(\omega . t + K.z)]\)
\(\frac{\partial \vec E}{\partial t} = \vec i . E_{io} . \omega [ - \sin (\omega . t - K . z) + \sin(\omega . t + K.z)]\)
Dans un milieu assimilé au vide, la vitesse de propagation étant \(\mathrm{c}\), la relation de Maxwell donne :
\(\overrightarrow{\mathrm{rot}} ~ \vec B = \mu_0 . \vec j + \mu_0 . \varepsilon_0 . \frac{\partial \vec E}{\partial t} = \mu_0 . \varepsilon_0 . \frac{\partial \vec E}{\partial t}\) en l'absence de courant (\(\vec j=0\))
\(\Rightarrow ~~ - \vec i . \frac{E_{io}}{\mathrm{c}} . K . [\sin (\omega . t - K . z) - \sin(\omega . t + K.z)] = \mu_0 . \varepsilon_0 . \vec i . E_{io} . \omega . [- \sin (\omega . t - K . z) + \sin(\omega . t + K.z)]\)
Sachant que :
\(\mu_0 . \varepsilon_0 = \frac{1}{\mathrm{c}^2}\) et que : \(\mathrm{c} = \frac{\omega}{K}\) , \(~ \Rightarrow ~ \frac{K}{\mathrm{c}} = \frac{\omega}{\mathrm{c}^2}\)
\(\Rightarrow ~~\) la relation de Maxwell est donc bien satisfaite.
Autre calcul possible, en utilisant la forme stationnaire de l'onde dans la région \((1)\) :
\(\vec E_1 (z, t) = 2 . E_{io} . \vec i . \sin (\omega . t) . \sin (K.z) ~~ \Rightarrow ~~ \mu_0 . \varepsilon_0 . \frac{\partial \vec E_1}{\partial t} = 2 . E_{io} . \mu_0 . \varepsilon_0 . \vec i . \omega . \cos (\omega . t) . \sin (K.z)\)
\(\overrightarrow{\mathrm{rot}} ~ \vec B = - \frac{\partial B_y}{\partial z} \vec i ~~~ \Rightarrow ~~ \mathrm{d}B_y = 2 . \mu_0 . \varepsilon_0 . \omega . E_{io} . \cos (\omega .t) . \sin (K.z) . \mathrm{d}z\)
[\(z\) seule variable d'intégration] \(~~~ \Rightarrow ~~ B_y = 2 \frac{\mu_0 . \varepsilon_0 . \omega}{K} \cos (\omega .t) . \cos (K.z)\)
Avec \(\mu_0 . \varepsilon_0 = \frac{1}{\mathrm{c}^2}\) et \(\frac{\omega}{K} = \mathrm{c}\) \(~~~ \Rightarrow ~~ \frac{\mu_0 . \varepsilon_0 . \omega}{K} = \frac{1}{\mathrm{c}}\) \(~~~ \Rightarrow ~~\) on obtient bien, par les équations de Maxwell, la même valeur de \(B_y\) que celle trouvée directement.
Superposition d'une onde progressive et d'une onde régressive de même amplitude (2)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Les plans métalliques situés en \(z=0\) et en \(z=L\) produisent des ondes réfléchies qui se superposent aux ondes incidentes.
Si la distance entre les plans métalliques est multiple de la demi-longueur d'onde, alors toutes les ondes progressives sont en phase, de même que toutes les ondes régressives sont en phase : leur somme est alors une onde stationnaire.