Polarisation par réflexion
Partie
Question
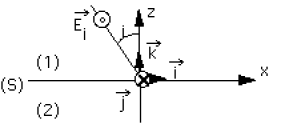
Figure 1
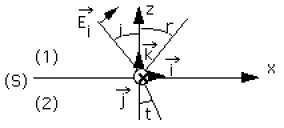
Figure 2
Soit \((S)\) le plan \((Z= 0)\) délimitant 2 diélectriques parfaits, non magnétiques de permittivité \(\varepsilon_0\) (resp. \(\varepsilon_2\)).
Notations : les composantes des champs seront désignées par 2 indices :
indice supérieur : \(x\) ou \(y\) ou \(z\)
indice inférieur : \(i\) (incident), ou \(r\) (réfléchi), ou \(t\) (transmis).
- A -
Une onde électromagnétique : plane, monochromatique, polarisée selon \(\vec j\) arrive sur ce plan (figure 1).
Donner l'expression du champ électrique incident \(\vec E_i\) .
Représenter les ondes réfléchie \(\vec E_r\) et transmise \(\vec E_t\) .
Montrer que la seule possibilité pour que soient satisfaites les conditions de continuité (de \(E\) tangentiel et de \(D\) normal) sur le plan de séparation \((S)\), est que \(\vec E_r\) et \(\vec E_t\) soient (comme \(\vec E_i\)) polarisés selon la direction \(\vec j\).
- B -
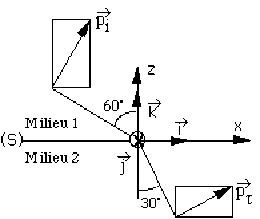
On considère maintenant une onde incidente électromagnétique : plane, monochromatique, et polarisée dans le plan \((x, z)\) (figure 2).
Représenter les ondes : réfléchie \(\vec E_r\) et transmise \(\vec E_t\).
Ecrire les relations de continuité sur le plan de séparation \((S)\).
En déduire la relation que doivent satisfaire \(e_1\), \(e_2\), \(\tan ~ i\), et \(\tan ~ t\) pour que l'onde réfléchie soit nulle.
En utilisant par ailleurs la loi de Descartes, en déduire qu'il existe un angle d'incidence \(i_B\) particulier (appelé incidence Brewsterienne) tel que \(E_R = 0\) .
Déterminer cet angle \(i_B\) en fonction de \(n_1\) et de \(n_2\) . Application numérique : \(n_1 = 1\) , \(n_2 = R(3)\) .
Quelle est, sous cette incidence, la relation entre les angles \(i_B\) et \(t\) ?
Représenter \(\vec E_i\) et \(\vec E_t\) dans le cas de l'application numérique précédente.
- C -
On considère maintenant un champ électromagnétique incident sous incidence Brewsterienne \(i_B\) , et ayant une composante \(\vec E_i \parallel \vec j\) et une composante \(\vec E_i' \perp \vec j\) .
Comment sera l'onde réfléchie par le plan ?
Comment peut-on appeler un tel dispositif ?
Aide simple
Revoir les conditions de réflexion sur un dioptre.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
On fait varier l'angle d'incidence alors que le champ électrique incident est polarisé parallèlement au dioptre.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
L'angle d'incidence est fixé égal à l'angle de Brewster, et on fait varier la direction de polarisation du champ électrique incident.
Rappel de cours
Voir la page Vibration polarisée et non-polarisée
Solution détaillée
-A- On suppose que \(\vec{E_i}\) est polarisé selon \(\vec j\) (figure 1)
A.1-
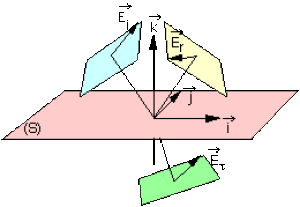
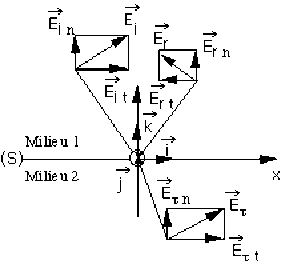
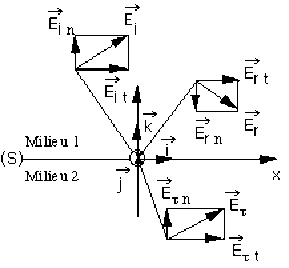
Champs électriques incident et réfléchi.
Notations :
les indices i, r, τ désignent respectivement les ondes incidente, réfléchie, transmise.
les indices n et t désignent respectivement les composantes normales et tangentielles.
les indices 1 et 2 désignent respectivement les grandeurs dans les régions (1) et (2).
Champ électrique incident : \(\vec{E_i}=E_{i0}\vec j\exp j(\omega t-K_i\vec{u_i}.\vec r)\)
Champ électrique réfléchi : \(\vec{E_r}=E_{r0}\vec{p_r}\exp j(\omega t-K_r\vec{u_r}.\vec r+\theta_r)\)
Champ électrique transmis : \(\vec{E_\tau}=E_{\tau0}\vec{p_\tau}\exp j(\omega t-K_\tau\vec{u_\tau}.\vec r+\theta_\tau)\)
La polarisation de ces champs est notée :
\(\vec{p_i}=\vec j\)
\(\vec{p_r}=\alpha_r\vec i+\beta_r\vec j+\gamma_r\vec k\)
\(\vec{p_\tau}=\alpha_\tau\vec i+\beta_\tau\vec j+\gamma_\tau\vec k\)
avec \(\alpha_r=\cos(\vec{p_r},\vec i)\) et idem pour les autres cosinus directeurs \(\beta_r,\gamma_r, a_\tau, b_\tau, g_\tau.\)
Figure 3
Champs représentés dans leur plan d'onde sans avoir tenu compte des conditions de réflexion sur le dioptre (S)
-A.2-
La réflexion de l'onde é.m. sur le dioptre (S) est soumise aux relations de continuité.
Les équations de Continuité donnent dans le plan (S)
\([\textrm{i.e } \vec r=0] \Rightarrow\begin{array}{ll} (1)&\overrightarrow{E_{1t}}=\overrightarrow{E_{2t}} \\\\ (2)&\overrightarrow{D_{1n}}=\overrightarrow{D_{2n}}\end{array}\Rightarrow (3)~ \varepsilon_1E_{1n}=\varepsilon_2E_{2n}\)
Remarque : dans la relation (3), et \(E_{1n}\) et \(E_{2n}\) désignent les composantes algébriques. On projette la relation (1) sur \(\vec i\)
\(\begin{array}{lll}\Rightarrow & \vec{E_{it}}.\vec i & = E_{i0}\vec j.\vec i\exp(j\omega t)+E_{r0}\alpha_r\exp j(\omega t+\theta_r)\\ & \vec{E_{2t}}.\vec i & =E_{\tau0}\alpha_\tau\exp j(\omega t+\theta_\tau)\end{array}\)
Donc, en \(t = 0\) sur le dioptre (S) \(\Rightarrow E_{r0} \alpha_r \exp j(\theta_r)=E_{\tau0} \alpha_\tau.\exp j(\theta_\tau)\) (4)
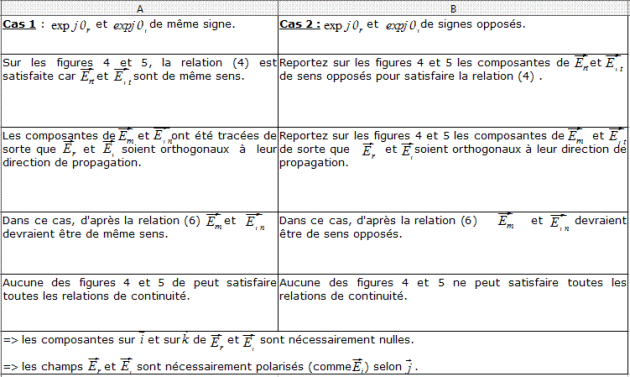
\(\Rightarrow\) Selon les valeurs des déphasages \(\theta_r\) et \(\theta_\tau\) des champs réfléchi et transmis par rapport au champ incident, les composantes sur \(\vec i\) des champs électriques réfléchi et transmis peuvent être de même sens ou de sens opposés. C'est ce que représentent les figures 4 et 5.
Dans la région 1, l'onde résultante est la superposition de l'onde incidente et de l'onde réfléchie et l'onde incidente est polarisée tangentiellement à (S).
Alors, la relation (3) donne \(\Rightarrow \begin{array}{lll} \varepsilon_1E_{1n}&=&e_1(0+\gamma_rE_{r0}\exp j(\omega t+\theta_r) \\ \varepsilon_2E_{2n}&=&e_2\gamma_\tau E_{\tau0}\exp j(\omega t+\theta_\tau)\end{array}\)
Donc, en \(t = 0\) sur le dioptre (S) \(\Rightarrow \varepsilon_1\gamma_rE_{r0}.e_2\alpha_\tau\exp j(\theta_r)=\varepsilon_2\gamma_\tau E_{\tau0}\exp j(\theta_\tau)\) (6)
\(\Rightarrow\) Selon les valeurs des déphasages \(\theta_r\) et \(\theta_\tau\) des champs réfléchi et transmis par rapport au champ incident, les amplitudes des champs électriques réfléchi et transmis peuvent être de même sens ou de sens opposés. C'est ce que représentent également les figures 4 et 5.
Hypothèses :
On admet que par réflexion sur un dioptre plan, une onde plane incidente donne naissance à une onde réfléchie plane et à une onde transmise plane.
On suppose que la propagation dans les milieux 1 et 2 peut se décrire par des champs réels, donc que les exponentielles qui interviennent ici sont réelles, donc que les déphasages sont soit nuls soit égaux à \(\pi\).
On suppose connue la structure de l'onde plane électromagnétique \(\Rightarrow\) le champ est transversal \(\Rightarrow\) les champs électriques sont perpendiculaires à leur direction de propagation.
Les figures 4 et 5 montrent les deux seuls cas possibles qui satisfassent ces conditions, en supposant que \(\vec{E_r}\) n'a pas de composante selon \(\vec j\) (autrement dit, en ne considérant que la composante sur \(\vec i\) ).
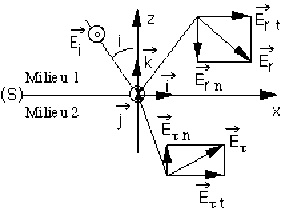
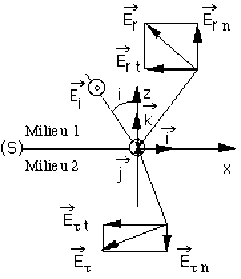
Remarque :
Les figures 4 et 5 représentent en réalité les champs dans le plan (S) du dioptre (en \(\vec r\) = 0) en tenant compte des conditions énoncées ci-dessus : sur ces figures les champs ont été "écartés" du plan (S) pour une simple raison de lisibilité.
Raisonnement :
-B- On suppose que \(\vec{E_{i}}\) est polarisé dans le plan (x, z). (figure 2).
-B.1-
Deux cas sont possibles :
Les 2 composantes \(\vec{E_{in}}\) et \(\vec{E_{rn}}\) sont selon \(\vec k \Rightarrow \vec{E_{\tau n}}\) doit être selon \(\vec k\)
Les 2 composantes \(\vec{E_{it}}\) et \(\vec{E_{rt}}\) sont selon \(\vec i \Rightarrow \vec{E_{rt}}\) doit être selon \(\vec i\)
-B.2-
Relations de continuité sur le dioptre \((r=0)\). La polarisation est dans le plan \(\Rightarrow\) \((x,z)\)
Elle est définie par les vecteurs unitaires ci-dessous :
\(\vec{p_i}=\alpha_i\vec i+\gamma_i\vec k\) avec \(\alpha_i=\cos i\) et \(\gamma_i=\sin i\)
\(\vec{p_r}=\alpha_r\vec i+\gamma_r\vec k\) avec \(\alpha_r=\cos r\) et \(\gamma_r=\sin r\)
\(\vec{p_\tau}=\alpha_\tau\vec i+\gamma_\tau\vec k\) avec \(\alpha_\tau=\cos t\) et \(\gamma_\tau=\sin t\)
Continuité des composantes tangentielles de \(\vec E \Rightarrow \vec{E_{1t}}=\vec{E_{2t}}\)
Projection sur \(\vec i\) (en \(t=0\) et \(\vec r=0\)) \(\Rightarrow \alpha_iE_{i0}+\alpha_rE_{r0}\exp j\theta_r=\theta_\tau E_{\tau0}\exp j\theta_\tau\) (7)
Projection sur \(\vec j\) (en \(t=0\) et \(\vec r=0\)) \(\Rightarrow \beta_rE_{r0}\exp j\theta_r=\beta_\tau E_{\tau0}\exp j\theta_\tau\) (8)
Continuité des composantes normales de \(\vec D \Rightarrow \vec{D_{1n}}=\vec{D_{2n}} \Rightarrow \varepsilon_1E_{1n}=\varepsilon_2E_{2n}\)
(en \(t=0\) et \(\vec r=0\)) \(\Rightarrow \varepsilon_1(\gamma_iE_{i0}+\gamma_rE_{r0}\exp j\theta_r)=\varepsilon_2\gamma_\tau E_{\tau0}\exp j\theta_\tau\) (9)
-B.3-
On suppose que l'onde réfléchie est nulle (\(\forall t\) et \(\forall r\)) \(\vec{E_r}=0 \Rightarrow E_{r0} =0\) et on va chercher si cette condition est possible.
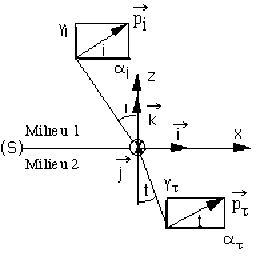
Figure 8
Vecteurs (unitaires) de polarisation des champs électriques incident et réfléchi
(7) \(\Rightarrow \alpha_iE_{i0}=\alpha_\tau E_{\tau0}\exp j\theta_\tau\)
(8) \(\Rightarrow 0=\beta_\tau E_{\tau0}\exp j\theta_\tau \Rightarrow \beta_\tau=0 \Rightarrow\) le champ électrique transmis est polarisé dans le plan (x,y)
(9) \(\Rightarrow \varepsilon_1\gamma_iE_{i0}=\varepsilon_2\gamma_\tau E_{\tau0}\exp j\theta_\tau\)
\(\frac{(9)}{(7)}=\varepsilon_1\frac{\gamma_i}{\alpha_i}=\varepsilon_2\frac{\gamma_\tau}{\alpha_\tau} \Rightarrow \varepsilon_1\tan i=\varepsilon_2\tan t\) (10)
-B.4-
On admet les lois de Descartes : \(n_1\sin i=n_2\sin t \Rightarrow \frac{\sin i}{\sin t}=\frac{n_2}{n_1}\) (11)
(10) \(\Rightarrow \frac{\tan i}{\tan t}=\frac{\varepsilon_2}{\varepsilon_1}\)
avec (11) \(\Rightarrow \frac{\tan i}{\tan t}=\frac{\sin i\cos t}{\sin t\cos i}=\frac{n_2\cos t}{n_1\cos i} \Rightarrow \frac{n_2\cos t}{n_1\cos i}=\frac{\varepsilon_2}{\varepsilon_1}\) (12)
(11) \(\Rightarrow \sin^2t=(\frac{n_1}{n_2})^2\sin^2i\)
(12) \(\Rightarrow \cos^2t=(\frac{n_1\varepsilon_2}{n_2\varepsilon_1})^2\cos^2i\)
(11)+(12) \(\Rightarrow 1=(\frac{n_1}{n_2})^2\sin^2i+(\frac{n_1\varepsilon_2}{n_2\varepsilon_1})^2\cos^2i=(\frac{n_1}{n_2})^2(1-\cos^2i)+(\frac{n_1\varepsilon_2}{n_2\varepsilon_1})^2\cos^2i\)
\(\Rightarrow 1-(\frac{n_1}{n_2})^2=(\frac{n_1}{n_2})^2.(-1+(\frac{\varepsilon_2}{\varepsilon_1})^2).\cos^2i\) (13)
Les relations \(\varepsilon\mu V^2=1 \Rightarrow \varepsilon_2\mu_0(\frac{c}{n_2})^2=1=\varepsilon_1\mu_0(\frac{c}{n_1})^2\) avec \(\mu=\mu_0\)
Les milieux 1 et 2 étant non magnétiques \(\Rightarrow \mu=\mu_0\)
En appelant V la vitesse dans un milieu caractérisé par \(\varepsilon\mu \Rightarrow \varepsilon\mu V^2=1 \Rightarrow \varepsilon=\frac{1}{\mu V^2}\)
Sachant que l'indice d'un milieu est défini par : \(n=\frac{c}{V} \Rightarrow V=\frac{c}{n} \Rightarrow \frac{\varepsilon_2}{\varepsilon_1}=(\frac{n_2}{n_1})^2\)
On porte ce résultat dans l'équation (13)
(13) \(\Rightarrow 1-(\frac{n_1}{n_2})^2=-(\frac{n_1}{n_2})^2\cos^2i(1-(\frac{n_2}{n_1})^4)=\cos^2i(-(\frac{n_1}{n_2})^2+(\frac{n_2}{n_1})^2)\)
\(\Rightarrow\) Il existe donc un angle d'incidence particulier : \(i=i_B\) appelé incidence Brewsterienne, défini par :
\(\cos^2i=\frac{1-(\frac{n_1}{n_2})^2}{(\frac{n_2}{n_1})^2-(\frac{n_1}{n_2})^2}\) pour lequel \(\vec{E_r}=0 \Rightarrow\) toute l'onde incidente est alors transmise.
Cette expression peut se simplifier : \(\cos^2i=\frac{\frac{n_2^2-n_1^2}{n_2^2}}{\frac{n_2^2}{n_1^2}-\frac{n_1^2}{n_2^2}}=\frac{\frac{n_2^2-n_1^2}{n_2^2}}{\frac{n_2^4-n_1^4}{n_1^2.n_2^2}}\)
\(\Rightarrow \cos^2i=\frac{n_2^2-n_1^2}{n_2^2}\frac{n_1^2.n_2^2}{n_2^4-n_1^4}=\frac{n_2^2-n_1^2}{n_2^2}\frac{n_1^2.n_2^2}{(n_2^2-n_1^2)(n_2^2+n_1^2)}=\frac{n_1^2}{n_1^2+n_2^2}\)
Application numérique : \((\frac{n_1}{n_2})^2=(\frac{1}{\sqrt{3}})^2=\frac{1}{3} \Rightarrow \cos i_B=\frac{1}{2} \Rightarrow \cos i_B=60^{\circ}\)
-B.5-
D'après la relation de Descartes : \(n_1\sin i_B=n_2\sin t_B\)
Application numérique : \(\begin{array}{llll} &\sin t_B=&\frac{n_1}{n_2}\sin i_B=\frac{1}{\sqrt{3}}.\frac{\sqrt{3}}{2}=\frac{1}{2} &\Rightarrow i_B=60^{\circ} \\ &\sin60^{\circ}=&\frac{\sqrt{3}}{2} &\Rightarrow t_B=30^{\circ}\end{array}\)
-C-
Sous incidence Brewsterienne :
\(\begin{array} {llll} \vec{E_i}=\vec{E_i}\parallel+\vec{E_i}\perp \textrm{ en notant } & \vec{E_i} || ~ \textrm{ la partie } ~||\vec j & \Rightarrow & \vec{E_i}|| ~ \in \textrm{ plan } (x,y) \\ & \vec{E_i}\perp ~ \textrm{ la partie } ~ \perp\vec j & \Rightarrow & \vec{E_i}\perp ~\in \textrm{ plan }(x,z) \end{array}\)
On a vu que sous incidence \(i_B~\Rightarrow\) la composante \(\vec{E_{i}} \perp \in\) plan \((x, z)\) n'est pas réfléchie, cette partie du champ électrique est totalement transmise.
Par contre, la partie \(\vec{E_{i}} ~||\) qui est dans le plan \((x,y)\) est en partie réfléchie, en partie transmise.
Comme on l'a vue dans la question -A2-, l'onde réfléchie est alors polarisée \(||\vec j\).
Ce dispositif (incidence d'une onde sous l'incidence de Brewster) est un polariseur par réflexion.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
L'animation montre la réflexion sur un dioptre plan et la réfraction d'une onde électromagnétique.
Le champ électrique est polarisé dans le plan d'incidence \(YOZ\). Dans ces conditions, il existe un angle d'incidence (incidence de Brewster) pour lequel l'amplitude de l'onde électromagnétique réfléchie est nulle.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Sous l'incidence de Brewster, ce n'est que si le champ électrique est polarisé dans le plan d'incidence que l'onde réfléchie à une amplitude nulle.
Pour une direction de polarisation quelconque du champ électrique incident, la composante dans le plan d'incidence du champ électrique est toujours nulle.
Autrement dit: s'il est non nul, le champ électrique réfléchi est polarisé selon \(OX\).